可微渲染入门笔记

本文讨论了可微渲染的入门，主体是 SIGGRAPH 2020 的 Differentiable Rendering Course 的阅读笔记。

这一笔记来自 SIGGRAPH 2020 的一篇 Course，Physics-based differentiable rendering: from theory to implementation. 笔记主要记了一下其中的理论推导部分，反正我目前没做可微渲染，后面具体上渲染方程的部分可以再看。

关于渲染的自动微分还可以看李子懋老师 2021 年的一篇 SIGGRAPH 文章 Systematically Differentiating Parametric Discontinuities，作者实现了一个用于 autodiff 的 Python DSL 为什么大家都这么喜欢 Python，可能对于 Luisa IR 的 autodiff 有帮助。

什么是可微渲染

给定所有参数 $\mathbb\pi$, 渲染得到图像 $I(\mathbf\pi)$, 与真实图像的 Loss 函数为 $L$, 那么可微渲染的目标就是计算 $\nabla_{\mathbf\pi}L(I(\mathbf\pi))$，从而使用基于梯度的方法优化渲染结果来实现逆向渲染。

对于 $\mathbf{\pi}$ 中的任何一个参数 $\pi$，我们都有 $$\frac{\partial}{\partial\pi}L(I(\mathbf\pi)) = \sum_i\frac{\partial L}{\partial I_i(\mathbf{\pi})}\frac{\partial I_i(\mathbf{\pi})}{\partial\pi}$$ 前者是简单的，譬如对最基本的 MSE Loss，有 $$L = \left(I(\mathbf\pi) - \hat I(\mathbf\pi)\right)^2$$

$$\frac{\partial L}{\partial I(\mathbf{\pi})} = 2\left(I(\mathbf\pi) - \hat I(\mathbf\pi)\right)$$

问题在于计算后者 $\frac{\partial I_i(\mathbf{\pi})}{\partial\pi}$

能不能把渲染「无痛」地变可微？

渲染本质上是积分问题，以一个简单的抗锯齿为例，如果每个像素只采样一个点，那么得到的结果就会有很多锯齿（高频噪声）。一个解决方案是套一个低通滤波器，也即对每个像素计算采样中心点附近的一个区域内的积分： $$I_i(\mathbf\pi) = \iint k(x,y)m(x_i+x, y_i+y; \mathbf\pi)\text{d}x\text{d}y = \iint f(x, y; \mathbf\pi)\text{d}x\text{d}y$$ 其中 $k$ 是卷积核，$m$ 是连续的像空间，$I$ 是离散的图片。实际渲染中，渲染器一般采用以下方法（即我们熟悉的「多重采样抗锯齿 MSAA」）来数值近似这个积分： $$\iint f(x, y; \mathbf\pi)\text{d}x\text{d}y \approx \frac{1}{N}\sum_{j=1}^N f(x_j, y_j; \pi)$$ 这个数值积分可以解决积分的计算，但是不能解决积分的微分问题： $$\frac{\partial}{\partial \pi_v}\iint f(x, y; \mathbf\pi)\text{d}x\text{d}y \not\approx \frac{1}{N}\sum_{j=1}^N \frac{\partial}{\partial \pi_v}f(x_j, y_j; \mathbf\pi) = 0$$

为什么离散采样的微分一定是 0？

$f(x_j, y_j; \mathbf\pi)$ 的值就是「这个点打到的物体的颜色」，如果 $\pi_v$ 改变后它打到的三角形不变，那么梯度必然是 0；如果正好跨过边界那么梯度理论上是无穷大——但是离散采样采到边界的概率是 0，因此可以不用管这一项。

因为微分本质上是考察局部变化，而离散的采样对局部变化不敏感，因此对离散采样的数值积分直接微分是不可行的。考察一个更简单的例子： $$\frac{\partial}{\partial p}\int_0^1(x < p\ ?\ 1:0) \text{d}x$$ 离散采样一定是 0，而实际结果是 1（因为后面这个积分就是 $p$）.

如何实现这个积分的微分？

计算离散的一元函数的积分的微分，可以先将其所有的间断点列出来，然后分别计算连续部分和间断点的微分.

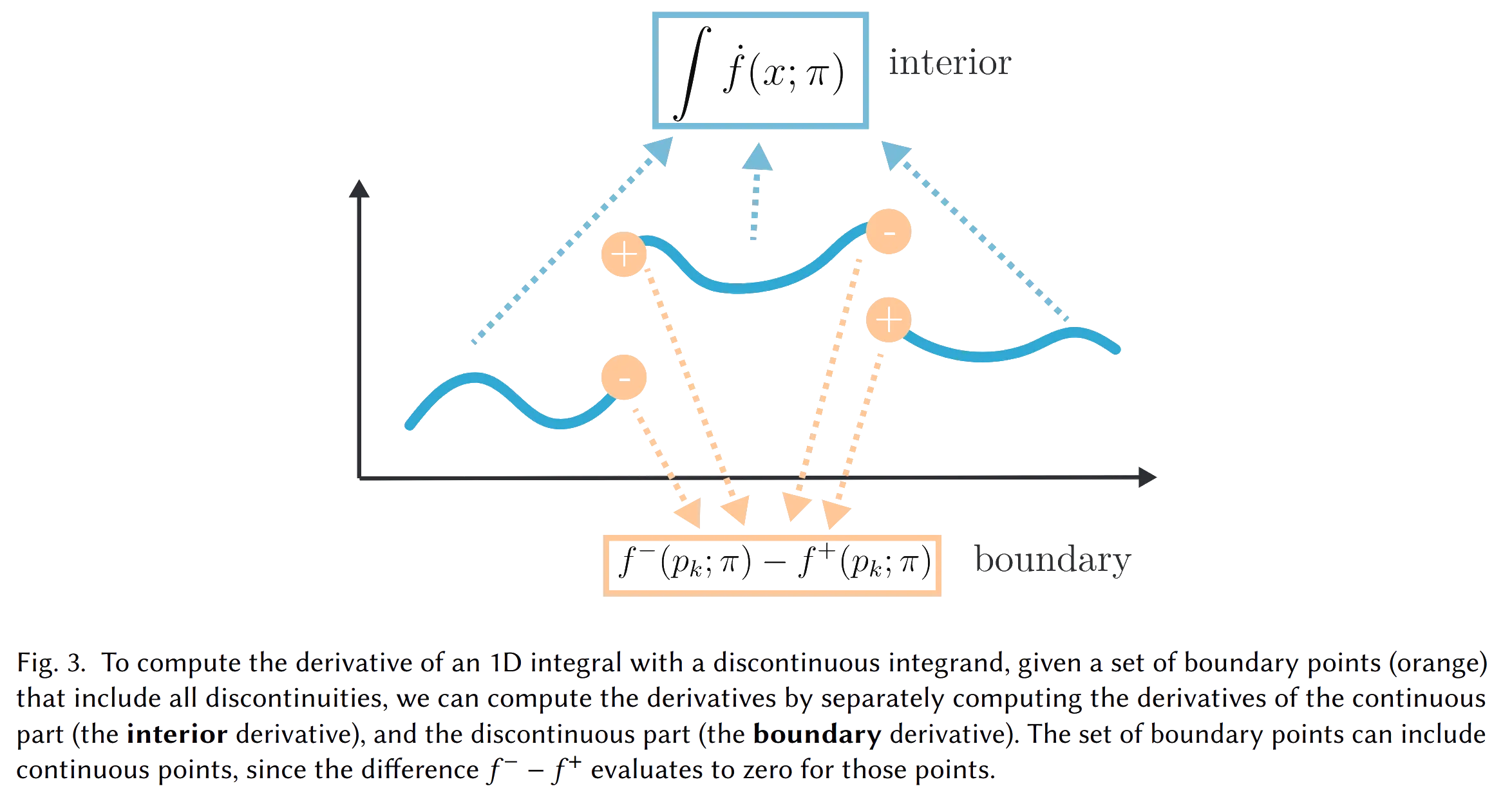
例如对于上面的积分 $$\frac{\partial}{\partial p}\int_0^1(x < p\ ?\ 1:0) \text{d}x = \frac{\partial}{\partial p}\int_0^p 1\text{d}x + \frac{\partial}{\partial p}\int_p^1 0\text{d}x$$ 然后再分别计算就可以了，一般地则有 $$\frac{\partial}{\partial\pi}\int_{a(\pi)}^{b(\pi)}f(x;\mathbf\pi)\text{d}x=\int_{a(\pi)}^{b(\pi)}\frac{\partial}{\partial\pi}f(x;\mathbf\pi)\text{d}x + \left[\frac{\partial b(\pi)}{\partial\pi}f(b(\pi); \mathbf\pi) - \frac{\partial a(\pi)}{\partial\pi}f(a(\pi); \mathbf\pi)\right]$$ 前者为内部项，后者为边界上的补偿

推广到高维……

令 $f$ 是定义在 $n$ 维流形 $\Omega(\pi)$ 上的函数，$\Gamma(\pi) \subset \Omega(\pi)$ 是一个 $n-1$ 维流形，包含 $\Omega(\pi)$ 的外部边界 $\partial\Omega(\pi)$ 和 $\Omega(\pi)$ 内部的不同区域间的边界，那么对 $f$ 在 $\Omega(\pi)$ 上积分的微分可以表示为： $$\frac{\partial}{\partial\pi}\left(\int_\Omega f\text{d}\Omega\right) = \int_\Omega\dot f \text{d}\Omega + \int_\Gamma\left\langle\mathbf{n}, \dot x\right\rangle \Delta f\text{d}\Gamma$$ 其中 $$\dot f = \frac{\partial f}{\partial\pi}$$ $$\dot x = \frac{\partial x}{\partial\pi} \$$ $$\Delta f(x) = \lim_{\epsilon\to0^-}f(x+\epsilon \mathbf n) - \lim_{\epsilon\to0^+}f(x+\epsilon \mathbf n)$$ 此处的 $\dot x$ 表示随着参数 $\pi$ 的移动 ，边界的移动方向，而上述积分的两部分可以分别数值积分近似： $$\int_\Omega\dot f \text{d}\Omega \approx \frac{1}{N_i}\sum_{j=1}^{N_i}\dot f(x_j)$$ $$\int_\Gamma\left\langle\mathbf{n}, \dot x\right\rangle \Delta f\text{d}\Gamma \approx \frac{1}{N_b}\sum_{j=1}^{N_b}\left\langle\mathbf{n}, \dot x\right\rangle\Delta f(x_j)$$ 因此我们解决了可微渲染的理论问题……