人工智能导论自救

6 June, 2021

This is one of the legacy posts

首先是喜闻乐见的吊图环节

第一章 搜索

A算法

启发式搜索算法， 对每个节点n，既维护一个从起点到n的路径长度值g(n)，又给出一个从n到终点的长度估计值h(n)，综合考虑f(n) = g(n) + h(n)来决定扩展次序。

记起点s到中间节点n的实际距离g*(n)，中间节点n到终点g的实际距离是h*(n)；起点s到中间节点n的估计距离g(n)，中间节点n到终点g的估计距离是h(n)。

实际的距离是f*(n) = g*(n) + h*(n)，估计的距离是f(n) = g(n) + h(n)

OPEN := {s}
CLOSED := {}
f(s) := g(s) + h(s)
while OPEN非空 do:
    n := OPEN中f值最小的节点
    if n为要寻找的节点 then
        return n
    将n从OPEN中移除
    将n加入CLOSED
    for m为n的邻居 do
        tent_g := g(n) + dist(n, m) //tent_g为途径n到m的路径长度
        if m既不在OPEN中又不在CLOSED中 then
            将m加入OPEN、标记n指向m
        else if m在OPEN中且tent_g < g(m) then
            标记n指向m
        else if m在CLOSED中且tent_g < g(m) then
            将m从CLOSED中移除、将m加入OPEN、标记n指向m
    将OPEN中的节点按照f排序
return FAILED

（我觉得马少平给的那个伪代码迷得一批）

A*算法

如果h*始终满足h(n) <= h*(n)，则称该算法为A*算法

两个结论：

1. 如果从初始节点s到目标节点g有路径，A*一定能找到最佳解
2. 如果h2(n) > h1(n)对非目标节点均成立，那么A1扩展的节点数 >= A2扩展的节点数

改进后的A*算法

A*算法有可能出现同一节点多次扩展的问题，可以进行以下改进：

1. 保证启发函数h有单调性：

   对于任意两个节点n_i和n_j，如果n_j是n_i的子节点，那么h(目标节点g) = 0且h(n_i) - h(n_j) <= dist(n_i, n_j)。

   可以证明，单调的估价函数一定满足A*条件

2. 将伪代码改为

   OPEN := {s}
   CLOSED := {}
   f(s) := g(s) + h(s)
   f_max := 0
   while OPEN非空 do:
       NEST := {OPEN集合中满足f值小于f_max的所有节点}
       if NEST非空 then
           n := NEST中g最小的节点
       else
           n := OPEN中f值最小的节点, f_max := f(n)
       // 原本是找f最小的，现在是在f足够小的里面找g最小的
       // 这样可以保障每次扩展到这个节点的时候，g都达到最优
       // 因此不需要多次扩展同一个节点
       if n为要寻找的节点 then
           return n
       将n从OPEN中移除
       将n加入CLOSED
       for m为n的邻居 do
           tent_g := g(n) + dist(n, m) //tent_g为途径n到m的路径长度
           if m既不在OPEN中又不在CLOSED中 then
               将m加入OPEN、标记n指向m
           else if m在OPEN中且tent_g < g(m) then
               标记n指向m
           else if m在CLOSED中且tent_g < g(m) then
               将m从CLOSED中移除、将m加入OPEN、标记n指向m
       将OPEN中的节点按照f排序
   return FAILED
   

第二章 对抗搜索

针对博弈问题：双人、一人一步、信息完备、零和

\(\alpha\)-\(\beta\)剪枝

对于每个节点都有一个估价。由于是一人一步，我们希望搜索树上偶数层达到极大值（对我方最有利），奇数层达到极小值（对对方最不利）。

对极大节点，我们维护其下界\(\alpha\)；对于极小节点，我们维护其上界\(\beta\)。

剪枝条件：

• 后辈节点的\(\beta\leq\)祖先节点的\(\alpha\)则产生\(\alpha\)剪枝，剪掉这个后辈节点的所有子节点。

  如果后辈节点的\(\beta\)比祖先的\(\alpha\)还小，这说明存在这个后辈节点的兄弟节点，这个兄弟节点的\(\beta\)（也就是祖先的\(\alpha\)）比后辈节点自己的\(\beta\)还大。一个理性的对手一定会走这个兄弟节点而不会走后辈节点自己，自然可以剪掉。

• 后辈节点的\(\alpha\geq\)祖先节点的\(\beta\)则产生\(\beta\)剪枝，剪掉这个后辈节点的所有子节点。

  如果后辈节点的\(\alpha\)比祖先的\(\beta\)还大，这说明存在这个后辈节点的兄弟节点，这个兄弟节点的\(\alpha\)（也就是祖先的\(\beta\)）比后辈节点自己的\(\alpha\)还大。理性的下棋者一定会选择这个兄弟节点而不会走后辈节点自己，自然可以剪掉。

\(\alpha\)-\(\beta\)剪枝的缺点：

• 对局面评估有过高的要求，需要大量专家知识，而且难以写出完美的估价函数

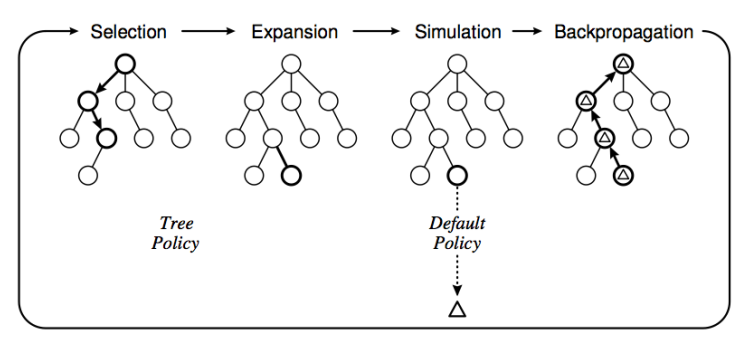
MCTS（蒙特卡洛树搜索）

1. 选择

   • 从根节点出发自上而下地选择一个落子点

   • 选择落子点时，使用这样一个公式计算权值，取出权值最大的一个：

     \(l_j = \overline X_j + c \sqrt{\frac{2\ln(n)}{T_j(n)}}\)

     其中\(\overline X_j\)是已经获得的回报的均值（守成项，胜率越高越倾向于选它）

     \(n\)是整棵树的访问总次数

     \(T_j(n)\)是这个节点访问的总次数

     \(c\)是一个加权项

2. 扩展

   • 向选定的点添加一个或多个子节点

3. 模拟

   • 对扩展出的节点用蒙特卡洛方法进行模拟

4. 回溯

   • 根据模拟结果依次向上更新祖先节点的估计值

第三章 高级搜索

针对的是最优化问题：

\(x\)为决策变量，\(D\)为定义域，\(f(x)\)为指标函数，\(g(x)\)为约束条件集合。那么，一个优化问题可以表示为求解满足\(g(x)\)的\(f(x)\)的最小值，即\(\min\limits_{x\in D}(f(x)\vert g(x))\)

如果定义域\(D\)上满足\(g(x)\)的解是有限的，那么称这是一个组合优化问题。

对于一个满足\(N:S\in D\to N(S)\in 2^D\)的映射\(N\)，我们称\(N(S)\)为\(S\)的邻域。

局部搜索（爬山）

始终朝着离目标更接近的方向走

x_b := 随机选D中的一个解
P := N(x_b)
while x_b 不满足结束条件 do
    选择P的子集P_1
    x_n := P_1中的最优解
    if f(x_n) < f(x_b) then //x_n比x_b更好
        x_b := x_n, P := N(x_b)
    else
        P := P - P_1
return x_b 

问题：可能只找到局部最优，找不到全局最优

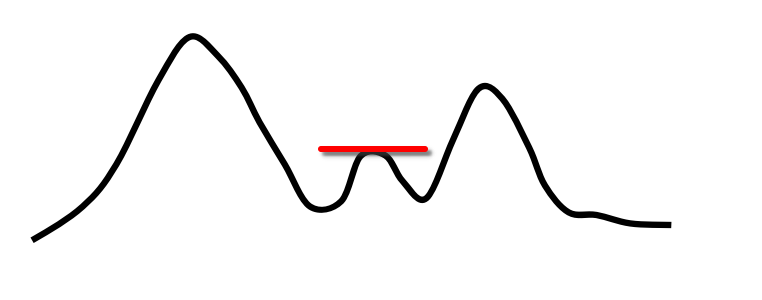
解决方案：改找最优为依概率采样，指标函数越好概率越大

问题：步长可能过长

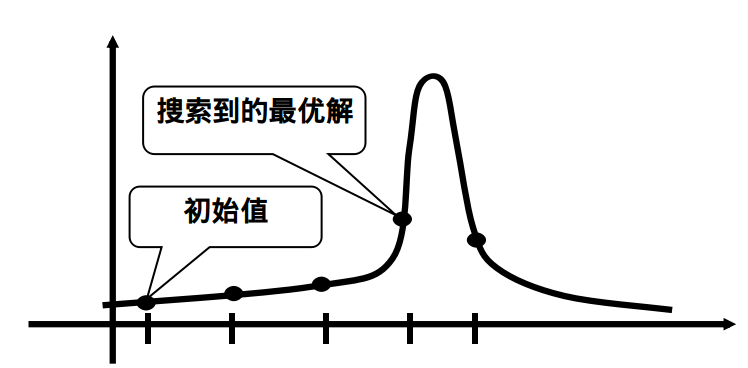
解决方案：变步长，越搜步长越短

问题：对起始点敏感，不同起始点找到的解可能不同

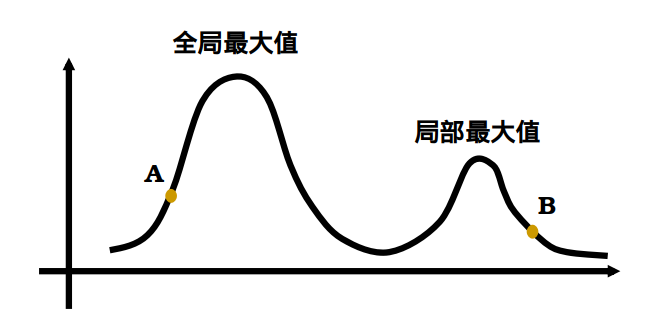
解决方案：多扔几个起始点，找最好的那个

模拟退火算法

i := 随机选D中的一个解
k := 0
t[0] := T_max
while f(i)不满足条件 do
    if 该温度下还未平衡 then
        从N(i)中随机选一个解j
        if f(j) < f(i) then //如果新的状态能量更低，直接转换
            i := j 
        else //如果新的能量更高，依概率转换
            P_i_to_j := e ^ - (f(j) - f(i)) / t
            if random(0, 1) < P_i_to_j then
                i := j
    t[k+1] := Drop(t[k]) //降温
    k := k + 1
return i

以概率1收敛于最优解（which means可能得到很差的解）

这必然是只记结论×

初温度选取：够高

给定一个比较大的接受频率\(P_0\)，则\(t_0 = \frac{\Delta f(i, j)}{\ln(P_0^{-1})}\)

\(\Delta f(i,j)\)可以有很多种估计，一个最简单的就是最大值减最小

温度下降

• 等比例，\(t_{k+1}=\alpha t_k\)

• 保证\(\frac{1}{1+\delta}\leq \frac{P_{t_k}(i)}{P_{t_{k+1}}(i)}\leq 1+\delta\)，一个充分条件是\(t_{k+1} = \frac{t_k}{1 + \frac{t_k \ln(1 + \delta)}{3\sigma t_k}}\)

终止条件

• 定长
• 接受率达到一定值
• 温度降低到阈值以下

遗传算法

好复杂………………要怎么考啊

第四章 统计学习方法

朴素Bayes方法

针对分类问题。

令输入空间为\(\mathbf{X}\subset R^n\)是n维向量的集合，输出空间为\(\mathbf{Y}={c_1,c_2,...,c_k}\)是类标记集合。

令\(X, Y\)分别为定义在\(\mathbf X, \mathbf Y\)上的随机变量，\(P(X,Y)\)为\(X,Y\)的联合分布，\(T={(x_1,y_1),...,(x_n,y_n)}\)为训练集（这里存在假设，T中的所有元素由联合分布\(P\)独立同分布采样得到，实际上这里不一定有独立性）。

由Bayes公式可以计算\(X\)的值确定后\(Y\)不同取值的概率： $$ P(Y=c_k\vert X=x) = \frac{P(X=x\vert Y=c_k)P(Y=c_k)}{\sum_kP(X=x\vert Y=c_k)P(Y=c_k)} $$ 因此在确定\(X\)的取值后，我们取出概率最大的label作为\(Y\)的估计值 $$ y = \arg\max\limits_{c_k}\frac{P(X=x\vert Y=c_k)P(Y=c_k)}{\sum_kP(X=x\vert Y=c_k)P(Y=c_k)} $$ 由于分母是一个定值，只需要取 $$ y = \arg\max\limits_{c_k}P(X=x\vert Y=c_k)P(Y=c_k) $$ \(P(X=x \vert Y=c_k)\)是难以计算的，复杂度随\(n\)指数级提升，因此引入独立性假设，假设\(X\)的各个维度是独立的，由此有 $$ \begin{align*} &P(X=x\vert Y=c_k) \ = &P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}\vert Y=c_k) \ = &\prod\limits_{j=1}^nP(X^{(j)}=x^{(j)}\vert Y=c_k)（这一步引入了独立性） \end{align*} $$ 故 $$ y = \arg\max\limits_{c_k}\prod\limits_{j=1}^nP(X^{(j)}=x^{(j)}\vert Y=c_k)P(Y=c_k) $$ 对于\(P(Y=c_k)\)，我们用极大似然进行估计（从结果来看就是频率估计概率……） $$ P(Y=c_k) = \frac{\sum\limits_{j=1}^nI(y_j=c_k)}{N}\ 当statement为真时，I(statement)=1，否则为0 $$ 实际应用中为了防止未出现的case使得概率降到0的情况，常添加平滑： $$ P_\lambda(X^{(j)}=a_{ji}\vert Y=c_k) = \frac{\sum\limits_{i=1}^nI(x_i^{(j)}=a_{ji},y_i=c_k)+\lambda}{\sum\limits_{i=1}^nI(y_i=c_k)+S_j\lambda}\ 其中S_j是第j个特征的取值数\ P_\lambda(Y=c_k)=\frac{I(y_i=c_k)+\lambda}{N+k\lambda}\ \lambda=1为Laplace平滑 $$

支持向量机

特征空间上的间隔最大化线性二分类器

这图竟然还有全家桶版本，属实是把美国政治玩明白了

线性可分支持向量机

目标：找一个最好的超平面把两种label隔开

定义线性可分训练集\(T={(x_1,y_1),...(x_N,y_N)}\)，其中\(x_i\in X=\mathbb{R}^n\)为特征向量，\(y_i\in {1,-1}\)为类标记（正标签/负标签，SVM是二分类器）。

通过间隔最大化得到分类超平面\(W^x+b^=0\)，对应的决策函数就是\(f(x)=\text{sgn}(W^x+b^)\)

何谓间隔？如何最大化？

超平面\((W, b)\)关于样本点\((x_i,y_i)\)的

• 函数间隔定义为\(\hat\gamma_i=y_i(Wx_i+b)\)
• 几何间隔定义为\(\gamma_i=y_i(\frac{W}{||W||}x_i+\frac{b}{||W||})\)

超平面\((W, b)\)关于训练集\(T\)的

• 函数间隔定义为\(\hat\gamma=\min\limits_i\hat\gamma_i\)
• 几何间隔定义为\(\gamma = \min\limits_i\gamma_i\)

注意到天然有\(\gamma_i = \frac{\hat\gamma_i}{||W||}\)

我们希望将几何间隔最大化（因为\(W\)和\(b\)是可以成比例缩放的，所以函数间隔是不能确定的，几何间隔可以看做某种归一化）。

常取\(\hat\gamma=1\)（成比例缩放不影响），问题转化为最大化\(\frac{1}{||W||}\)，也就是最小化\(\frac{1}{2}||W||^2\)，换言之，问题规约为

求\(\min\limits_{W,b}\frac{1}{2}||W||^2\)，使得\(y_i(Wx_i+b)\geq 1, i=1,2,...,n\)

使得不等式中等号成立的点就构成了支持向量（Support Vectors）。

学习过程

用Lagrange乘子法，定义Lagrange函数\(L(W,b,\alpha)=\frac{1}{2}||W||^2+\sum\limits_{i=1}^N\alpha_i[1-y_i(Wx_i+b)]\)

其中\(\alpha_i\)是\(\alpha\)的各分量（即\(\alpha=(\alpha_1,...,\alpha_N)^T\)）

转为求\(\min\limits_{W,b}\max\limits_\alpha L(W,b,\alpha)\)

注意到有\(\min\limits_{W,b}L(W,b,\alpha)\leq L(W,b,\alpha)\leq \max\limits_\alpha L(W,b,\alpha)\)恒成立，因此有\(\min\limits_{W,b}\max\limits_\alpha L(W,b,\alpha)\leq \max\limits_\alpha\min\limits_{W,b} L(W,b,\alpha)\)

当满足KKT条件的时候，上式等号成立，可以通过求解对偶问题\(\max\limits_\alpha\min\limits_{W,b} L(W,b,\alpha)\)来解决原问题。

KKT条件：

• \(\nabla_{W,b}L(W,b,\alpha)=0\)
• \(\alpha_i[1-y_i(Wx_i+b)]=0\)
• \([1-y_i(Wx_i+b)]\leq 0\)
• \(\alpha_i\geq 0\)

对于\(\max\limits_\alpha\min\limits_{W,b} L(W,b,\alpha)\)，可以先对内部\(\min\limits_{W,b} L(W,b,\alpha)\)的求偏导并代入，问题变为求

\(\max\limits_\alpha -\frac{1}{2}\sum_\limits{i=1}^{N}\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum\limits_{i-1}^N\alpha_i, s.t.; \sum\limits_{i=1}^N\alpha_iy_i=0,\alpha_i\geq 0, i=1,2,...,N\)

也就是

\(\arg\min\limits_\alpha \frac{1}{2}\sum_\limits{i=1}^{N}\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum\limits_{i-1}^N\alpha_i, s.t.; \sum\limits_{i=1}^N\alpha_iy_i=0,\alpha_i\geq 0, i=1,2,...,N\)

得到最优解\(\alpha^=(\alpha_1^,\alpha_2^,...,\alpha_N^)^T\)，\(W^=\sum\limits_{i=1}^N\alpha_i^y_ix_i\)，选择一个下标\(j\)使得\(0\lt \alpha_i^\lt C\)，\(b^=y_j-\sum\limits_{i=1}^Ny_i\alpha^_i(x_i\cdot x_j)\)（不同的下表计算出的\(b^\)是一致的）

线性支持向量机

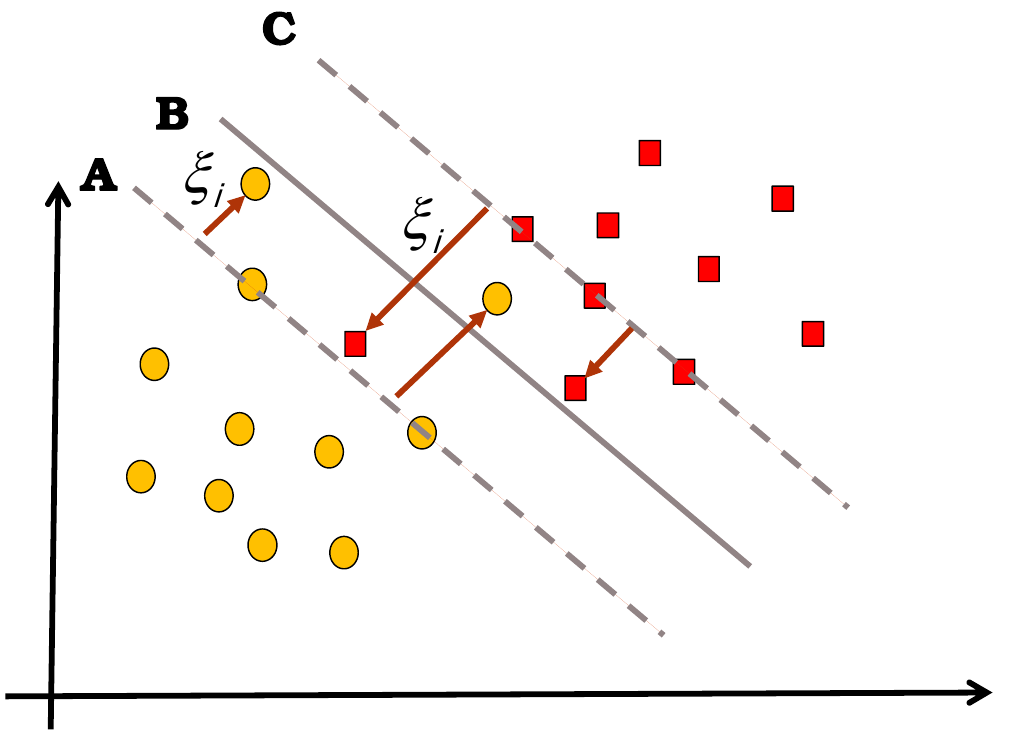
有可能不再可分，即有些点不满足\(y_i(Wx_i+b)\geq 1\)了。

因此对于每个点\((x_i,y_i)\)我们引入松弛变量\(\xi_i\)，保证每个点\(y_i(Wx_i+b)\geq 1 - \xi_i\)的同时优化\(\xi_i\)使其最小，优化目标改为\(\min\limits_{W,b,\xi}(\frac{1}{2}||W||^2+c\sum\limits_{i=1}^N\xi_i)\)，（其中\(c>0\)是惩罚参数，\(c\)越大对误分类惩罚越大，用\(c\)来处理间隔大和误分类点少的平衡）

类似上面的做法，问题归约为（注意这里和可分的SVM唯一区别是\(\alpha\)有了范围限制） $$ \arg\min\limits_\alpha \frac{1}{2}\sum_\limits{i=1}^{N}\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum\limits_{i-1}^N\alpha_i, s.t.; \sum\limits_{i=1}^N\alpha_iy_i=0,0\leq \alpha_i\leq C, i=1,2,...,N $$ 得到最优解\(\alpha^=(\alpha_1^,\alpha_2^,...,\alpha_N^)^T\)，\(W^=\sum\limits_{i=1}^N\alpha_i^y_ix_i\)，选择一个下标\(j\)使得\(0\lt \alpha_i^\lt C\)，\(b^=y_j-\sum\limits_{i=1}^Ny_i\alpha_i^(x_i\cdot x_j)\)（不同的下表计算出的\(b^\)是一致的）

超平面仍然是\(W^x+b^=0\)，决策函数仍然是\(\text{sgn}(W^x+b^)\)

\(\alpha_i^*\gt 0\)对应的\(x_i\)是（软间隔的）支持向量

• 若\(\alpha_i^*=0\)，则不是支持向量（对应上图曲线外侧的点）

• 若\(0<\alpha_i^*<C\)则\(\xi_i=0\)，\(x_i\)在间隔边界上，是支持向量（对应上图两条虚线上的点）

• 若\(\alpha_i^*=C\)，\(x_i\)也是支持向量

  • 若\(0\lt \xi_i\lt 1\)则分类正确（对应上图在己方虚线和实线之间的点）
  • 若\(\xi_i=1\)则在超平面上（对应上图在实线上的点）
  • 若\(\xi_i\gt 1\)则被误分（对应上图在实线和对方虚线之间的点）

非线性支持向量机

一般的方法是把线性不可分的东西经过变换映射到一个新的空间上去，在新的空间上它线性可分。

具体操作时，一般给定一个核函数\(K(x_i,x_j)\)，把空间变换和内积放到一起去，这样问题转化为求

$$ \arg\min\limits_\alpha \frac{1}{2}\sum_\limits{i=1}^{N}\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum\limits_{i-1}^N\alpha_i, s.t.; \sum\limits_{i=1}^N\alpha_iy_i=0,0\leq \alpha_i\leq C, i=1,2,...,N $$

得到最优解\(\alpha^=(\alpha_1^,\alpha_2^,...,\alpha_N^)^T\)，\(W^=\sum\limits_{i=1}^N\alpha_i^y_ix_i\)，选择一个下标\(j\)使得\(0\lt \alpha_i^\lt C\)，\(b^=y_j-\sum\limits_{i=1}^Ny_i\alpha_i^*K(x_i,x_j)\)，决策函数是\(\text{sgn}(\sum\limits_{i=1}^N\alpha_i^y_iK(x_i,x)+b^)\)

注：函数\(K\)为核函数，当且仅当存在\(\phi:X\to H\)，使得\(\forall x,z\in X, K(x,z)=\phi(x)\cdot\phi(z)\)

常用核函数包括：

• 多项式核函数\(K(x,z)=(x\cdot z+1)^p\)
• 高斯核函数\(K(x,z)=\exp\left(-\frac{\Vert x-z\Vert^2}{2\sigma^2}\right)\)

决策树

内部节点表示一个特征/属性，叶子节点表示一个类

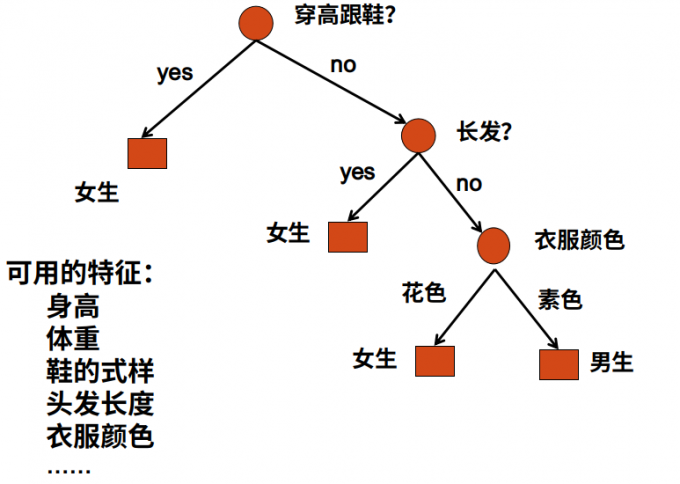
对于给定的训练集，我们可以构造出多个决策树，一般而言目标是然损失函数最小。从所有决策树中选出最佳决策树是NPC问题（实际上也会过拟合），所以我们一般采取启发式方法，转为寻找近似解。

决策树的学习一般包括以下三部分：

• 特征选择
• 决策树生成
• 决策树剪枝

特征选择

不一定要用所有特征，而是用分类能力较强的特征。分类能力的强弱一般用信息增益来衡量，指特征A加入后对数据集D进行分类的不确定性减少的程度

首先，随机变量\(X\)的熵定义为\(H(X)=-\sum\limits_{i=1}^np_i\log p_i\)，其中\(p_i=P(X=x_i)\)。如果概率由数据集\(D\)估计得到，熵也记为\(H(D)\)。

条件熵\(H(Y|X)=\sum\limits_{i=1}^nP(X=x_i)H(Y|X=x_i)=\sum\limits_{x,y}p(x,y)\log\frac{p(x)}{p(x,y)}\) ，表示给定X的情况下Y的不确定性。

（注：\(H(Y|X=x_i)=\sum\limits_yp(y|x)\log p(y|x)\)）

特征A对数据集D的信息增益定义为\(g(D,A)=H(D)-H(D|A)\)，越大表明添加特征A后信息增益越多

其中两个具体熵的计算公式如下：

设训练集D，K个类\(Ck\)，特征A有n个不同的取值{ai,…,an}，A的不同取值将D划分为n个子集D1…Dn，Di中属于类Ck的样本的集合为\(D_{ik}\)，|·|表示样本个数。 $$ H(D)=-\sum_{k=1}^K\frac{|C_k|}{|D|}\log_2\frac{|C_k|}{|D|}（C_k是第k个类别的集合 $$ $$ H(D|A) = -\sum_{i=1}^n\frac{|D_i|}{|D|}\sum_{k=1}^K\frac{|D_{ik}|}{|D_i|}\log_2\frac{|D_{ik}|}{|D|} $$ $$ g(D,A)=H(D)-H(D|A) $$

决策树生成

ID3算法

D为训练集，A为特征集，阈值\(\epsilon>0\)

额外定义D中实例数最多的类标签为C_m

function ID3(D, A, epsilon, C_m) do
    if D中所有实例都是同一类C_k then 
        T := 类标记为C_k的单节点树
        return T
    if A = {} or D = {} then //什么特征也没有，D为空可能在递归时出现
        T := 类标记为D中实例数最多的类C_m的单节点树 //哪个多蒙哪个
        return T
    A_g := 集合A中满足信息增益g(D,A_i)最大的特征
    if g(D,A_g) < epsilon then //这个特征是个铁废物
        T := 类标记为D中实例数最多的类C_m的单节点树 //还是哪个多蒙哪个
        return T
    else
        对于A_g的所有可能取值a_i，将集合D划分为若干子集D_i不相交的并
        for D_i in D的划分 do
            T_i := ID3(D_i, A-{A_g}, epsilon, C_m)
        T := 以T_i为子节点的树
        return T

缺点：信息增益倾向于选择分支比较多的属性

C4.5算法

定义信息增益比： $$ g_R(D,A)=\frac{g(D,A)}{H_A(D)} $$ $$ H_A(D) = -\sum_{k=1}^n\frac{|D_k|}{|D|}\log_2\frac{|D_k|}{|D|} $$ 将上面ID3算法中的信息增益直接替换为信息增益比即可。

另外，对于非离散的属性，C4.5的处理方法是找到一个值\(a_0\)，将不大于它和大于它的分为左右子树。

缺点：倾向于选择分割不均匀的特征

解决方法：先选出若干信息增益大的特征，再从这些里面选择信息增益比最大的

决策树剪枝

后剪枝：从已经生成的树上剪掉一些节点，将父节点作为新的叶子。

数据量不同的情况下剪枝方法不同：

• 数据量足够大，可以分为训练验证和测试
  • 首先用训练集训练
  • 从下向上剪枝，同时在验证集上测试性能，直到验证集上性能开始下降为止
  • 在测试集上测试，作为系统性能
• 数据量不够大，只有训练集合
  • 计算每个节点的经验熵（给定参数a）
  • 从下而上回缩，如果回缩后损失函数变小，那么剪枝
  • 直到不能继续为止

其中损失函数和经验熵定义如下： $$ C_a(T)=\sum_{t=1}^{|T|}N_tH_t(T)+a|T|，为参数a确定后的损失函数 $$ $$ H_t(T)=-\sum_k\frac{N_{tk}}{N_t}\log\frac{N_{tk}}{N_t}，为经验熵 $$ $$ C(T)=\sum_{t=1}^{|T|}N_tH_t(T)=-\sum_{t=1}^{|T|}\sum_{k=1}^KN_{tk}\log\frac{N_{tk}}{N_t}表示模型对训练数据的预测误差 $$ $$ C_a(T)=C(T)+a|T|，即损失一部分来自预测误差，另一部分来自模型本身的复杂程度 $$