Paper Note: Generalized Resampled Importance Sampling - GRIS theory

15 October, 2024

这篇文章的内容主要分为两个部分：第一部分是对 ReSTIR 采样理论的补完，将自己视为 Importance Resampling for Global Illumination 中 RIS 理论的扩展，提出所谓的 GRIS or Generalized RIS 理论；另一部分则是将这个理论应用在 path 复用上提出 ReSTIR PT。

这篇笔记集中于 GRIS 理论的讨论。

RIS 理论基础

背景

渲染本质是积分。要对函数 $f$ 进行积分（即计算 $I = \int_\Omega f(x) \text{d}x$），则需要使用 MC 积分器，先采样本之后计算

$$ \langle I\rangle = \sum_{i=1}^M \frac{f(X_i)}{p(X_i)} $$

那么只要分布 $p$ 的 support 覆盖函数 $f$ 的 support，就有

$$ E[\langle I \rangle] = \int_\Omega f(x)\text {d}x $$

即可以实现无偏估计。但在无偏估计的基础上，$p$ 和 $f$ 相差越大，MC 积分的方差越大，而方差在渲染结果上表现为噪声，因此我们希望分布 $p$ 尽可能地逼近 $f$.

问题 - 所有样本同分布的情况

给定一组样本 $X_1, X_2, ..., X_M$，所有样本独立且均服从分布 $p$，要在样本中依据一定的权重 $w_i$ 重采样 $Y$，使得 $Y$ 的概率密度接近目标函数 $\hat p = f$。

我们给定权重

$$ w_i = \frac{1}{M} \hat p(X_i) W_i $$

其中

$$ W_i = \frac{1}{p(X_i)} $$

从 $X_1,X_2,...,X_M$ 中按照权重 $w_i$ 采样得到样本 $Y$，并定义 unbiased contribution weight 为

$$ W_Y = \frac{1}{\hat p(Y)} \sum_{i=1}^M w_i $$

那么只要随机变量 $Y$ 的 support 覆盖函数 $f$ 的 support，我们就有 $E[f(Y)W_Y] = I$

正确性证明

$$ \begin{aligned} E[f(Y)W_Y] &= E\left[f(Y) \cdot \frac{1}{\hat p(Y)} \cdot \sum_{i=1}^M w_i\right] \\ &= E\left[ \sum_{i=1}^M w_i \cdot \frac{f(X_i)}{\hat p(X_i)} \right] \\ &= \frac{1}{M} E\left[ \sum_{i=1}^M\frac{f(X_i)}{p(X_i)} \right] \\ &= \frac{1}{M} \sum_{i=1}^M E\left[ \frac{f(X_i)}{p(X_i)} \right] \\ &= \int_\Omega f(x) dx \end{aligned} $$

这样采样仍然保证无偏。

问题 - 泛化，各样本分布不同的情况

给定一组样本 $X_1, X_2, ..., X_M$，其中 $X_i$ 服从分布 $p_i$，要在样本中依据一定的权重 $w_i$ 重采样，使得重采样的概率密度接近目标函数 $\hat p$

为了在不同分布中进行 balance，我们引入 MIS weight

$$ m_i(x) = \frac{p_i(x)}{\sum_{j=1}^M p_j(x)} $$

注意到它天然满足 $\sum_{i=1}^M m_i(x) = 1$，引入 MIS 后的权重定义为

$$ w_i = m_i(X_i) \hat p(X_i) W_i $$

其中

$$ W_i = \frac{1}{p_i(X_i)} $$

退化形式

当所有 $p_i = p$ 的时候 $m_i = \frac{1}{M}$，MIS 情形退化回之前的朴素情形

unbiased contribution weight 保持不变，我们仍然有 $E[f(Y)W_Y] = I$

正确性证明

$$ \begin{aligned} E[f(Y)W_Y] &= E\left[f(Y) \cdot \frac{1}{\hat p(Y)} \cdot \sum_{i=1}^M w_i\right] \\ &= E\left[ \sum_{i=1}^M w_i \cdot \frac{f(X_i)}{\hat p(X_i)} \right] \\ &= E\left[ \sum_{i=1}^M m_i(X_i)\frac{f(X_i)}{p_i(X_i)} \right] \\ &= \sum_{i=1}^ME\left[ m_i(X_i)\frac{f(X_i)}{p_i(X_i)} \right]\\ &= \sum_{i=1}^M \int_\Omega m_i(x)\frac{f(x)}{p_i(x)} \cdot p_i(x) \text{d} x \\ &= \sum_{i=1}^M\int_\Omega m_i(x) f(x) \text{d} x \\ &= \int_\Omega \sum_{i=1}^M m_i(x) f(x) \text{d} x \\ &= \int_\Omega f(x) \text{d}x \end{aligned} $$

注意：

求和号和期望的换序来自样本的独立性
各个样本对应的积分区间其实并不相同，因此要保证正确性需要 support 覆盖

即所有 $p_i$ 的 support 之并能覆盖函数 $f$ 的 support，即 $\forall x \in \text{supp}(f), \exists, p_i ; \text{s.t. } x\in \text{supp}(p_i)$

Generalized RIS

在多分布 RIS 的基础上，本文提出了 Generalized RIS 用来处理不同 domain 上的 reuse 问题。

背景

在简单的情形（如 ReSTIR DI）中，采样目标是光源分布，不同 pixel 对应的 target domain 是完全相同的。在更加复杂的复用中则不然，例如使用 ReSTIR 复用路径，采样目标是每个 pixel 的路径空间，相邻两个 pixel 的路径空间显然不同。在这种情况下我们就需要一个将其他空间中的样本 map 到自己的目标空间的方式，即 shift mapping.

形式定义

假定 $f$ 的定义域是 $\Omega$，要复用样本 $X_s \in \Omega_s$，我们需要定义 shift mapping $T: \Omega_s \to \Omega$

这个映射的要求如下
- （如果元素 x 存在 map）确定性，一对一，可逆
- （如果元素 x 不存在 map）不能有其他元素 map 到 x
本质上是 $\Omega_s$ 子集到 $\Omega$ 子集的一个双射，但可以有洞

引入 $T$ 之后的权重进一步定义为

$$ w_i = m_i(T_i(X_i)) \hat p(T_i(X_i)) W_i \cdot |\partial T_i/\partial X_i| $$

注意此处 $T_i$ 的 Jacobian 行列式！

我们从映射后的样本 $Y_1,Y_2,...,Y_M$ 中采样，$Y_i = T_i(X_i)$，权重为 $w_i$

$W_i$ 的定义维持不变，仍然是

$$ W_i = \frac{1}{p_i(X_i)} $$

unbiased contribution weight 保持不变，我们仍然有 $E[f(Y)W_Y] = I$

退化形式

如果 $\Omega_i = \Omega$ 且 $T = id$ 那么 Generalized RIS 退化回 RIS

正确性证明

$$ \begin{aligned} E[f(Y)W_Y] &= E\left[f(Y) \cdot \frac{1}{\hat p(Y)} \cdot \sum_{i=1}^M w_i\right] \\ &= E\left[ \sum_{i=1}^M w_i \cdot \frac{f(X_i)}{\hat p(X_i)} \right] \\ &= E\left[ \sum_{i=1}^M m_i(T_i(X_i)) f(T_i(X_i)) \left|\frac{\partial T_i}{\partial x}\right|\right] \\ &= \sum_{i=1}^ME\left[ m_i(T_i(X_i)) f(T_i(X_i)) \left|\frac{\partial T_i}{\partial x}\right|\right] \\ &= \sum_{i=1}^M \int_{\Omega_i} m_i(T_i(x)) f(T_i(x)) \left|\frac{\partial T_i}{\partial x}\right| \text{d} x \\ &= \sum_{i=1}^M \int_{\Omega} m_i(y) f(y) \text{d} y \\ &= \int_{\Omega} \sum_{i=1}^M m_i(y) f(y) \text{d} y \\ &= \int_{\Omega} f(y) \text{d} y \end{aligned} $$

里面的三个重点：

交换求和号与期望是因为各样本的独立性
出现 $y$ 的那一步应用了换元积分法，令 $y = T_i(x)$，Jacobian 正好凑出一个 $\text{d} y$
最后一步仍然需要保证 $T_i$ 的像集之和覆盖 $\Omega$
- 实际应用中每个 pixel 都有来自自己的 sample，所以一定会有一个 $\Omega_i = \Omega, T_i = id$，因此这个条件理论上是天然保证了的

含 Shift Mapping 时 MIS 的必要性

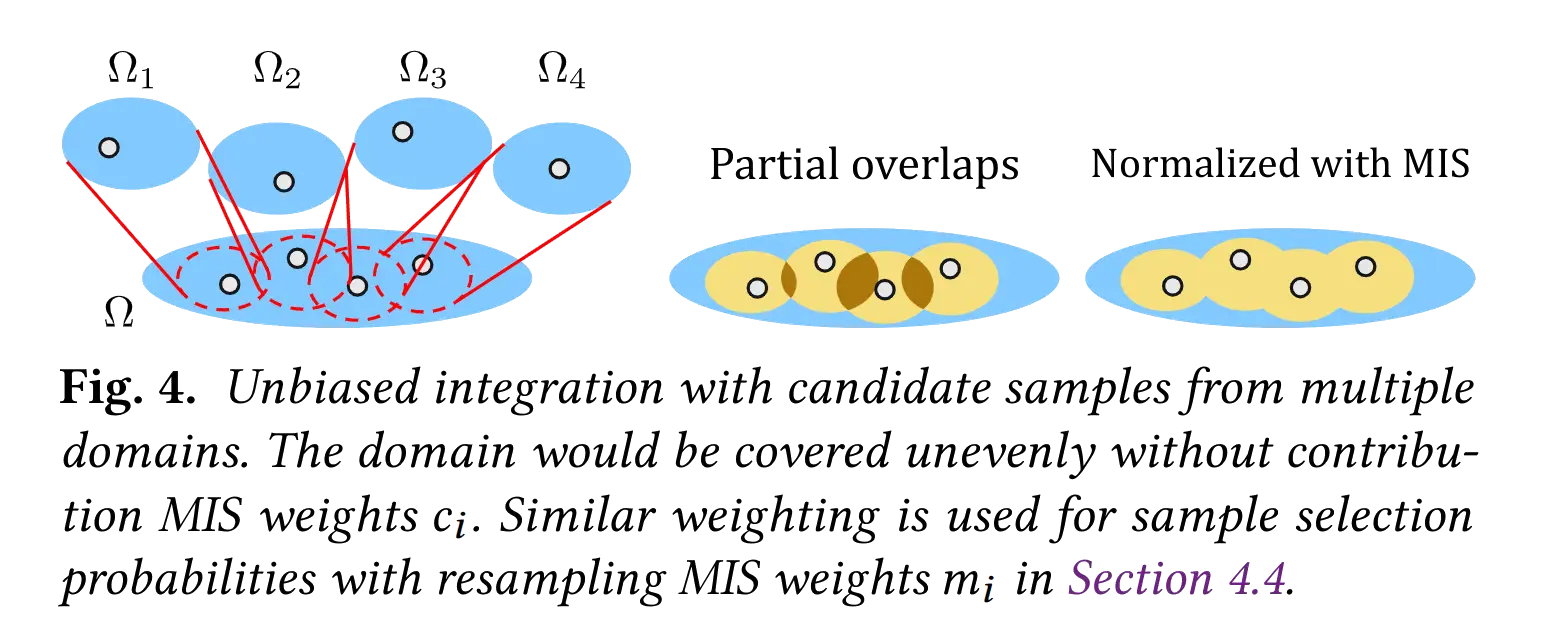
$\Omega$ 里的一个 sample 可能来自多个 $\Omega_i$，因此必须要 MIS 来进行 balance —— 否则我们 MC 积分器里的估计项 $\frac{f(Y)}{p_Y(Y)}$ 中的 $p_Y$ 会不准确，进而导致偏差

ReSTIR - As Chained GRIS

利用扩展后的 GRIS，ReSTIR 可以被描述为一个 GRIS 链：

令 $Y_i^{t-1}$ 是像素 $i$ 在帧 $t-1$ 处的一条路径（采样/重采样得到的均可），reservoir 里保存着它的 unbiased contribution weight $W_{Y_i^{t-1}}$，在帧 $t$ 处我们有

（初始采样）对每个像素 $i$ 采样得到当前帧该像素的一个独立 sample $X_i^t$ 并计算它的 contribution weight $W_{X_i^t}$
（时间复用）用 GRIS 在 $Y_i^{t-1}$ 和 $X_i^t$ 之间进行重采样得到 $Z_i$ - 可能会用 motion vector warp 旧像素
（空间复用）每个像素选一些邻居 $j$，在 $Z_i$ 和邻居 $Z_j$ 之间 GRIS 重采样得到 $Y_i^t$
（输出）计算 $f_i(Y_i^t) W_{Y_i^t}$ 为积分的估计值