Radiative Backpropagation 阅读笔记

9 February, 2023

本文讨论了用于可微渲染的 Radiative Backpropagation。

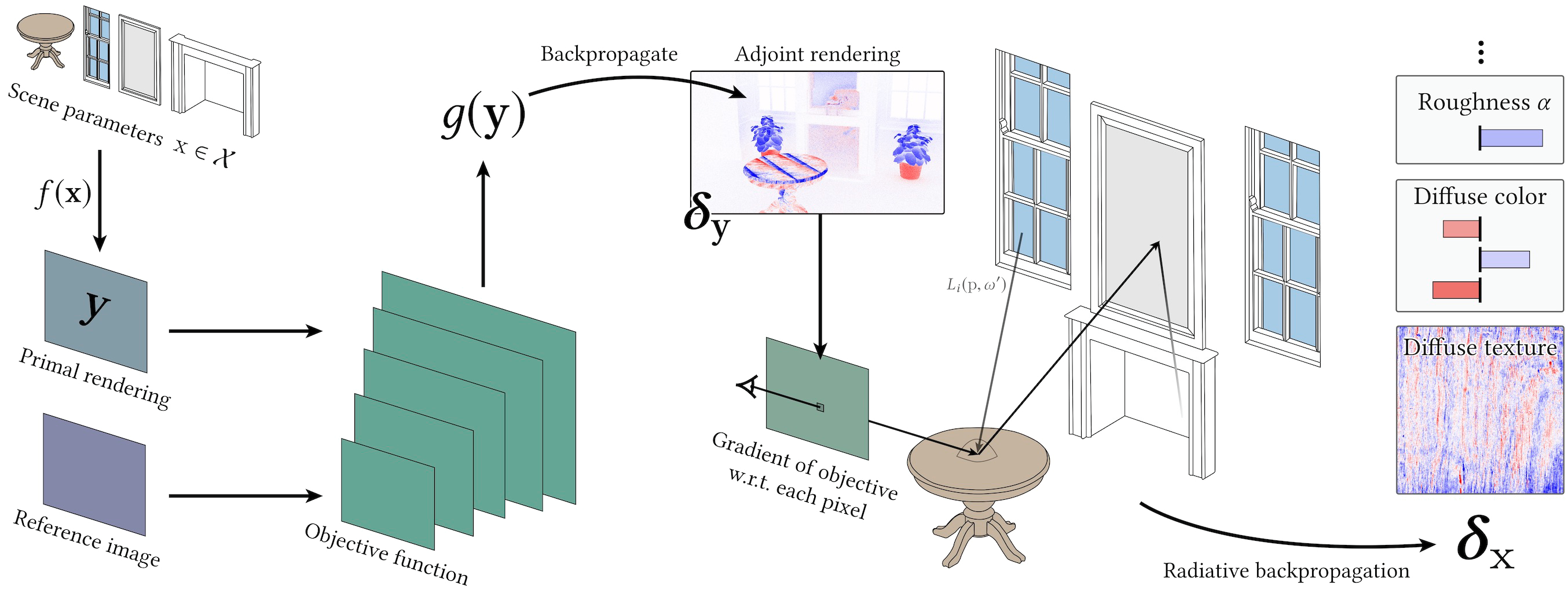
引入

将场景参数形式化为 \(\mathbf{x}\)，渲染函数形式化为 \(f\)，计算 \(\mathbf{y} = f(\mathbf{x})\) 的过程就是正向渲染的过程。

可微渲染试图计算 $$ \mathbf{J}_f := \frac{\partial f(\mathbf{x})}{\mathbf x} $$ 由于 \(\mathbf{x}, \mathbf{y}\) 的空间都很高维，直接计算 \(\mathbf{J}_f\) 不可行，因此现有方法主要分为以下两种：

• 前向 (forward-mode) 方法，计算微小扰动 \(\mathbf{\delta_x}\) 对 \(\mathbf{y}\) 的影响 \(\mathbf{\delta_y} = \mathbf{J}_f\mathbf{\delta_x}\)
• 反向 (reverse-mode) 方法，计算使 \(\mathbf{y}\) 产生变化 \(\mathbf{\delta_y}\)，\(\mathbf{x}\) 需要做出的微小扰动 \(\mathbf{\delta_x} = \mathbf{J}_f^T\mathbf{\delta_y}\)

以计算 \(y = x_0 \times x_1 + x_2\) 的梯度为例，前向和反向方法的计算流程分别如图所示：

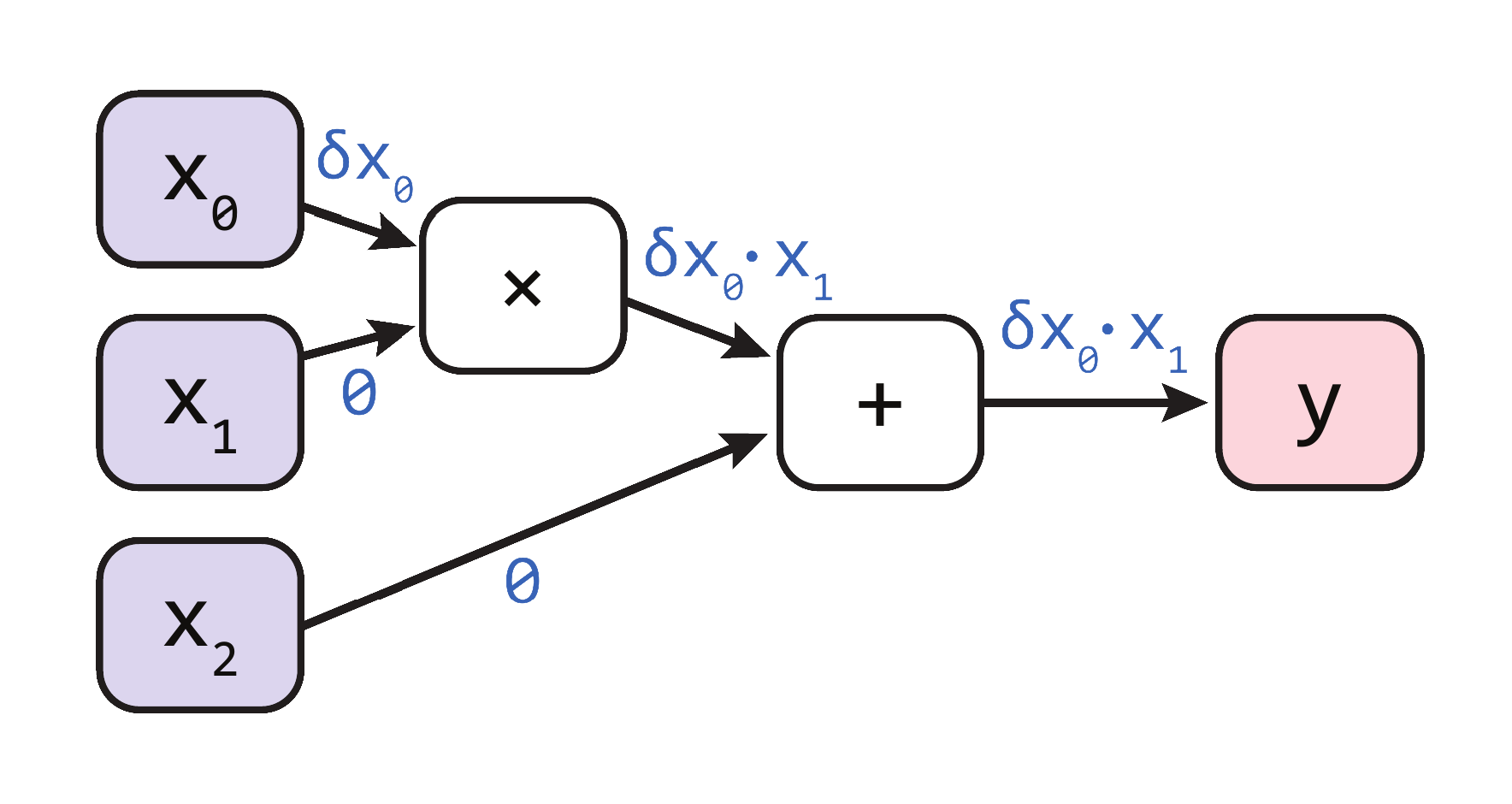
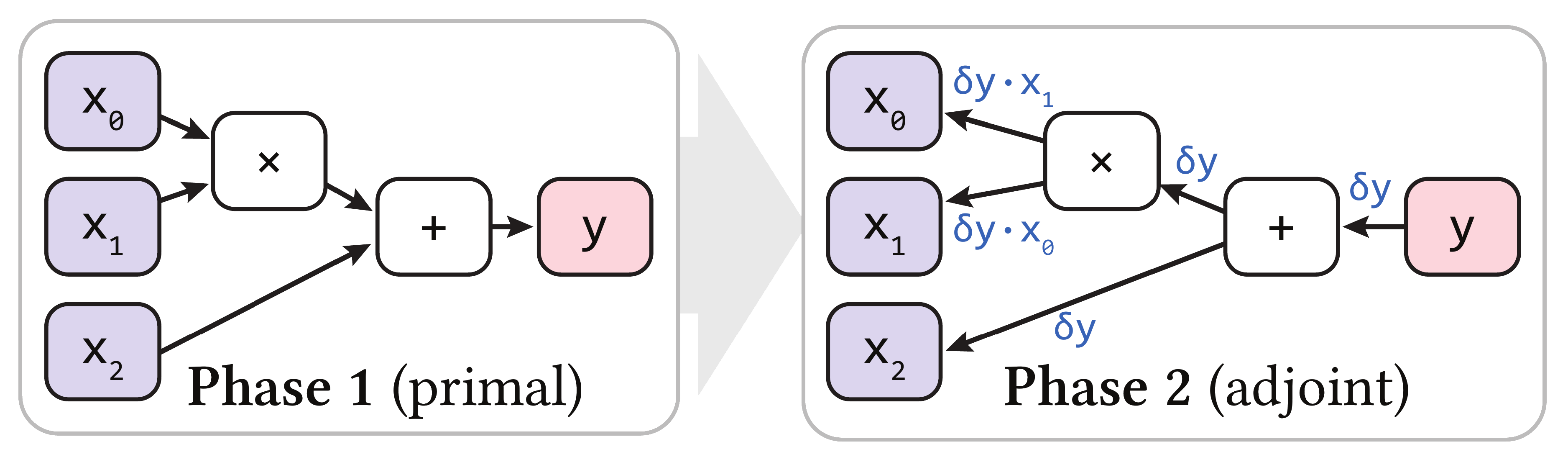
反向方法中，最常见的做法就是基于 tracing 的 auto-differentiation，即在正向计算时记录计算图，然后反向传播。然而，这一方法要求前向计算时在计算图上记录大量信息，使其内存消耗极高且计算缓慢。

Radiative Backpropagation 的提出就提供了一种内存和时间开销都较小的反向方法计算梯度，它不需要在前向计算时记录计算图，而是先预计算部分内容，并在前向渲染完成后再进行反向传播。

理论

假设

推导时进行了以下假设：

• 不考虑体效应 (volumetric effects)
• 不考虑剪影 (silhouette) 边界引起的梯度

渲染的三个基本等式

测量 (Measurement) 等式

记图像中每个像素为 \(I_1, I_2, \cdots, I_n\)，第 \(k\) 个像素的的测量值为 \(W_k\) 和 \(L_i\) 在空间 \(\mathcal{A} \times S^2\)的内积，即 $$ I_k = \left\langle W_k, L_i\right\rangle = \int_{\mathcal{A}}\int_{S^2}W_k(\mathbf{p},\mathbf{\omega})L_i(\mathbf{p},\mathbf{\omega})\text{d}\mathbf{\omega}^{\perp}\text{d}\mathbf{p} $$ 其中 \(W_k\) 是 \(I_k\) 的重要性函数，\(L_i\) 是入射辐照度，\(\mathcal{A}\) 表示所有点，\(S^2\) 表示半球面。

传输 (Transport) 等式

对于未受遮挡的光线，其入射辐照度与射出点的出射辐照度相等，即 $$ L_i(\mathbf{p},\mathbf{\omega}) = L_o(\mathbf{r}(\mathbf{p},\mathbf{\omega}), -\mathbf{\omega}) $$ 其中 \(\mathbf{r}(\mathbf{p},\mathbf{\omega})\) 表示沿着光线 \((\mathbf{p},\mathbf{\omega})\) 能找到的最近的与平面的交点，也就是这条光线的射出点。

注意到，不考虑遮挡这一假设在这里起了作用。

散射 (Scattering) 等式

对于一个点，它的出射辐照度与入射辐照度的关系可以表示为 $$ L_o(\mathbf{p},\mathbf{\omega}) = L_e(\mathbf{p},\mathbf{\omega}) + \int_{S^2}L_i(\mathbf{p},\mathbf{\omega'})f_s(\mathbf{p},\mathbf{\omega},\mathbf{\omega'})\text{d}\mathbf{\omega'}^{\perp} $$ 其中 \(L_e(\mathbf{p},\mathbf{\omega})\) 为自发光，\(f_s(\mathbf{p},\mathbf{\omega},\mathbf{\omega'})\) 为 BSDF，此等式即我们常说的「渲染方程」。

三个等式的微分形式

为了方便，记偏微分算子 \(\frac{\partial}{\partial \mathbf{x}}\) 为 \(\partial_\mathbf{x}\)

测量等式

$$ \partial_{\mathbf{x}}I_k = \int_{\mathcal{A}}\int_{S^2}W_k(\mathbf{p},\mathbf{\omega})\partial_\mathbf{x}L_i(\mathbf{p},\mathbf{\omega})\text{d}\mathbf{\omega}^{\perp}\text{d}\mathbf{p} $$

注意到此处没有 \(W_k\) 的梯度，这也是因为我们不考虑遮挡，因此重要性是不变的

传输等式

$$ \partial_\mathbf{x}L_i(\mathbf{p},\mathbf{\omega}) = \partial_\mathbf{x}L_o(\mathbf{r}(\mathbf{p},\mathbf{\omega}), -\mathbf{\omega}) $$

散射等式

$$ \partial_\mathbf{x}L_o(\mathbf{p},\mathbf{\omega}) = \partial_\mathbf{x}L_{e}(\mathbf{p},\mathbf{\omega}) + \int_{S^2}[\partial_\mathbf{x}L_i(\mathbf{p},\mathbf{\omega'})f_s(\mathbf{p},\mathbf{\omega},\mathbf{\omega'}) + L_i(\mathbf{p},\mathbf{\omega'})\partial_\mathbf{x}f_s(\mathbf{p},\mathbf{\omega},\mathbf{\omega'})]\text{d}\mathbf{\omega'}^{\perp} $$

等式右侧出现了三个含有 \(\partial_{\mathbf{x}}\) 的项：

• \(\partial_{\mathbf{x}}L_e(\mathbf{p},\mathbf{\omega})\)

  如果场景参数 \(\mathbf{x}\) 发生扰动时光源的亮度发生了变化，它会「发射」微分辐照度 (differential radiance)

• \(\partial_\mathbf{x}L_i(\mathbf{p},\mathbf{\omega'})f_s(\mathbf{p},\mathbf{\omega},\mathbf{\omega'})\)

  微分辐照度也会像一般辐照度一样被「散射」

• \(L_i(\mathbf{p},\mathbf{\omega'})\partial_\mathbf{x}f_s(\mathbf{p},\mathbf{\omega},\mathbf{\omega'})\)

  如果场景参数 \(\mathbf{x}\) 发生扰动材质发生了变化，这个 BSDF 也会 「发射」的微分辐照度

优化微分的计算

给定优化目标，我们记损失函数为 \(g\)，渲染函数为 \(f\)，需要计算的就是 $$ \partial_{\mathbf{x}}g(f(\mathbf{x})) = \mathbf{J}_{g \circ f}(\mathbf{x}) = \mathbf{J}_g(f(\mathbf{x}))\mathbf{J}_f(\mathbf{x}) $$ 我们将它分为两步计算：

• 首先计算 \(\mathbf{\delta_y} = \mathbf{J}^T_g(\mathbf{y})\)，这个可以手搓也可以自动微分

• 然后用 radiative backpropagation 计算 \(\mathbf{\delta_x} = \mathbf{J}^T_f\mathbf{\delta_y}\)

\(\mathbf{J}^T_f\mathbf{\delta_y}\) 的计算

将 \(\mathbf{J}_f\) 写成列向量的形式为

$$ \mathbf{J}_{f} = [\partial_{\mathbf{x}}I_0, \cdots, \partial_{\mathbf{x}}I_n] $$

因此

$$ \mathbf{J}^T_f\mathbf{\delta_y} = \sum_{k=1}^n\mathbf{\delta}_{\mathbf{y},k}\partial_{\mathbf{x}}I_k = \int_{\mathcal{A}}\int_{S^2}\left[\sum_{k=1}^n\mathbf{\delta}_{\mathbf{y},k}W_k(\mathbf{p},\mathbf{\omega})\right]\partial_\mathbf{x}L_i(\mathbf{p},\mathbf{\omega})\text{d}\mathbf{\omega}^{\perp}\text{d}\mathbf{p} $$

定义「释放伴随辐照度」

$$ A_e(\mathbf{p},\mathbf{\omega}) := \sum_{k=1}^n\mathbf{\delta}_{\mathbf{y},k}W_k(\mathbf{p},\mathbf{\omega}) $$ 在计算出 \(\mathbf{\delta_y}\) 之后 \(A_e\) 就是可平凡计算的了。

那么我们参考测量等式，可以将其记为

$$ \mathbf{J}^T_f\mathbf{\delta_y} = \langle A_e, \partial_{\mathbf{x}}L_i \rangle $$

再记

$$ \mathbf{Q}(\mathbf{p},\mathbf{\omega}) := \partial_{\mathbf{x}}L_e(\mathbf{p},\mathbf{\omega}) + \int_{S^2}L_i(\mathbf{p},\mathbf{\omega'})\partial_{\mathbf{x}}f_s(\mathbf{p},\mathbf{\omega},\mathbf{\omega'})\text{d}\mathbf{\omega'}^{\perp} $$

另外定义两个算子，散射算子 \(\mathcal{K}\) 和传播算子 \(\mathcal{G}\) 为

$$ (\mathcal{K}h)(\mathbf{p},\mathbf{\omega}) := \int_{S^2}h(\mathbf{p},\mathbf{\omega'})f_s(\mathbf{p},\mathbf{\omega},\mathbf{\omega'})\text{d}\mathbf{\omega'} $$

$$ (\mathcal{G}h)(\mathbf{p},\mathbf{\omega}) := h(\mathbf{r}(\mathbf{p},\mathbf{\omega}), -\mathbf{\omega}) $$

那么根据以上三个定义可以得到两个等式，

$$ \partial_{\mathbf{x}}L_i = \mathcal{G}\partial_{\mathbf{x}}L_o $$ $$ \partial_{\mathbf{x}}L_o = \mathcal{K}\partial_{\mathbf{x}}L_i + \mathbf{Q} $$

分别对应传输等式和散射等式。根据 Veach 1997 年的一篇文章，我们可以直接得到一些结论，如

$$ \partial_{\mathbf{x}}L_o = \mathcal{KG}\partial_{\mathbf{x}}L_o + \mathbf Q = (I - \mathcal{KG})^{-1}\mathbf{Q} = \sum_{i=0}^{\infty}(\mathcal{KG})^i\mathbf Q $$

记 \(\mathcal S := (I - \mathcal{KG})^{-1}\)，那么有 \(\mathcal {G, K, GS}\) 均为自伴随 (self-adjoint) 线性算子

若线性算子 \(\mathcal O\) 满足 \(\forall v_1, v_2\) 均有 \(\langle \mathcal Ov_1, v_2\rangle = \langle v_1,\mathcal{O}v_2\rangle\)，则称它为自伴随的

因此

$$ \mathbf{J}^T_f\mathbf{\delta_y} = \langle A_e, \partial_{\mathbf{x}}L_i \rangle = \langle A_e, \mathcal{GS}\mathbf{Q} \rangle = \langle \mathcal{GS}A_e, \mathbf{Q} \rangle $$

对 \(A_e\) 做 \(\mathcal{GS}\) 算子结果不变，本质上表明，其实我们可以「从另一侧开始」散射和传播辐照度，结果不变。而因为 \(A_e\) 是标量函数而 \(\mathbf Q\) 是维度和 \(\mathbf{x}\) 相同的矢量函数（根本无法计算），应用自相关性质之后它变得容易计算得多。

在有了 \(A_e\) 之后再定义类似的「入射伴随辐照度、出射伴随辐照度」 \(A_i, A_o\)，满足

$$ A_i = \mathcal{G}A_o $$ $$ A_o = \mathcal{K}A_i + A_e $$

这样我们就有了同样满足渲染基本等式的伴随辐照度 \(A_e, A_o, A_i\)，将反向传播变成了「另一次前向渲染」。

伪代码

def grad(x):
    # 前向渲染
    y = f(x)
    # 计算 y 的微分
    delta_y = J_g(y)
    # 用 radiative backprop 计算 x 的微分
    return radiative_backprop(x, delta_y)

def radiative_backprop(x, delta_y):
    delta_x = 0
    for _ in range(num_samples):
        # 重要性采样一条光线
        p, omega, weight = sensor.sample_ray()
        # 计算释放伴随辐照度
        weight *= A_e(delta_y, p, omega) / num_samples
        # 在场景中传播伴随辐照度
        delta_x += radiative_backprop_sample(x, p, omega, weight)
    return delta_x

def radiative_backprop_sample(x, p, omega, weight):
    # 反向找到交点
    p_prime = r(p, omega)
    # 如果这个点有释放辐照度（光源），那么把这部分对微分的贡献加上
    delta_x = adjoint([[ L_e(p_prime, -omega) ]], weight)
    # 从 BSDF 上采样一条光线
    omega_prime, bsdf_value, bsdf_pdf = sample(f_s(p_prime, -omega, ·))
    # 如果这个 BSDF 对微分有贡献，则加上
    delta_x += adjoint([[ f_s(p_prime, -omega, omega_prime) ]],
                       weight * L_i(p, omega_prime) / bsdf_pdf)
    
    # 递归
    return delta_x + radiative_backprop_sample(x, p_prime, omega_prime, 
                                               weight * bsdf_value / bsdf_pdf)

上面出现了两个 adjoint([[ q(z) ]], delta)，它的语义是将梯度 \(\mathbf{\delta}\) 传播至 \(q\)（通过计算 \(\mathbf{J}_q^T(\mathbf{x},\mathbf{z})\mathbf{\delta}\)），然后返回关于 \(\mathbf{x}\) 的梯度。

优化

使用有偏梯度估计加速

把 \(\mathbf{Q}\) 的定义从

$$ \mathbf{Q}(\mathbf{p},\mathbf{\omega}) := \partial_{\mathbf{x}}L_e(\mathbf{p},\mathbf{\omega}) + \int_{S^2}L_i(\mathbf{p},\mathbf{\omega'})\partial_{\mathbf{x}}f_s(\mathbf{p},\mathbf{\omega},\mathbf{\omega'})\text{d}\mathbf{\omega'}^{\perp} $$

改为

$$ \mathbf{Q}_{\text{approx}}(\mathbf{p},\mathbf{\omega}) := \partial_{\mathbf{x}}L_e(\mathbf{p},\mathbf{\omega}) + \int_{S^2}\partial_{\mathbf{x}}f_s(\mathbf{p},\mathbf{\omega},\mathbf{\omega'})\text{d}\mathbf{\omega'}^{\perp} $$

即直接去掉入射辐照度（将它变为1），这样做的好处是 radiative backprop 时不必递归计算入射辐照度。

神奇的是，它不仅算得快了，还收敛得快了。

复用中间结果加速

作者注意到 radiative backprop 的过程中，许多中间结果和前向渲染是相同的（例如 BSDF 采样结果、MIS 权重等），因此我们可以直接把 backprop 和下一次前向渲染一起做了，只采样一次。

这样的本质是用上一次迭代的 \(\mathbf{y}\) 的梯度去传播这次 \(\mathbf{x}\) 的梯度，在梯度变换平稳的情况下这样做是可以的。

此时的伪代码是

def grad_optimized(x):
    y = f(x)
    while not converged:
        delta_y = J_g(y)
        # radiative backprop 的时候会把下一个 y 也一起渲染出来
        y, delta_x = radiative_backprop(x, delta_y)
        # 传播梯度 ...