ReSTIR GI: Path Resampling for Real-Time Path Tracing 阅读笔记

6 August, 2023

本文讨论了 ReSTIR GI，即使用 ReSTIR 方法维护 probe 的采样来处理 1 bounce 全局光照的算法。

写在前面

这个是把 ReSTIR 采样器进行推广的工作，使得 ReSTIR 可以用于全局光照。文章整体比较简单，也比较短，也没做出什么理论上的创新（可能就是因为这个没发 SIGGRAPH 而是发了 HPG）。

简单地说就是先得到一张包含每个像素 visible point 的空间位置+局部法线的 G Buffer（光栅化或者 ray tracing 直接光照），然后从每个 visible point 出发随机采样出一个间接光的入射点作为 sample point，然后对 sample point 进行愉快的 ReSTIR。

吊诡的是，ReSTIR GI 采样的目标分布可以非常简单（比如直接设置为\(\hat p\propto L_o(x_s,-\omega_i)\)，BRDF 和余弦几何项都不包含）而仍然取得很好的效果。作者解释为简单的目标分布能使一个像素产生的样本对于其他像素而言更加有效。而且由于 sample point 的 \(L_o\) 是被缓存的，作者不得不假定当 sample point 连接不同 visible point 时 \(L_o\) 是不变的——这一假定在 sample point 位于非 diffuse 介质的情况下是假的，如果场景里 glossy 多会导致 artifact。

算法流程

与 ReSTIR DI 不同，ReSTIR GI 需要维护三个图像大小的 Buffer，分别用于存储当前轮随机采样得到的 initial sample buffer，上一轮留下的 temporal reservoir buffer 和用于存储邻居像素采样信息的 spatial reservoir buffer。

一个像素对应的 SAMPLE 数据结构的定义如下，每个 buffer 都由 width * height 个 SAMPLE 组成。

要进行 ReSTIR GI 计算，首先算法需要拿到一张保存了各像素着色点（称为 visible point）的位置和法线的 G Buffer，随后每一轮算法都包含三步：

• 初始采样
• 时间重采样
• 空间重采样

算法的大致流程可以描述为这两张图：

初始采样

从每个 visible point 出发，以初始分布 \(p_q\) 采样方向 \(\omega_i\)。\(p_q\) 可以是一个非常垃圾的分布，BRDF、余弦加权甚至平均采样都可以。从 visible point \(x_v\) 出发向 \(\omega_i\) 方向追踪，得到交点 \(x_s\) 作为像素 \(q\) 的 sample point。

随后，算法估计从 \(x_s\) 出发 \(-\omega_i\) 方向（即到 \(x_v\) ）的出射辐照度 \(L_o\) 作为 \(x_v\) 受到的间接光照。如果 \(L_o\) 用直接光照计算，算法得到的就是 1 bounce GI；如果 \(L_o\) 用 \(n\) bounce 的 PT w. NEE 计算，那么算法得到的就是 \(n+1\) bounce GI。注意到这里 \(L_o\) 只保存了一个值而没有保存方向，因此后面 \(x_s\) 连接其他像素的 \(x_v\) 时也会用这个值——也就是默认了不同方向的 \(L_o\) 相同。

初始采样的结果会放入 initial sample buffer。

初始采样的伪代码如下：

时间重采样

要进行重采样首先要确定目标分布\(\hat p\)，它可以是理想的 \(\hat p\propto L_o(x_s,\omega_i)f(\omega_o,\omega_i)\langle\cos\theta_i\rangle\)（类似 ReSTIR DI），也可以是简单的 \(\hat p\propto L_o(x_s,\omega_i)\)。

时间重采样就是简单地取出 temporal reservoir buffer，将它与 initial sample buffer 对应位置的 reservoir 混合，然后放回原位置，伪代码如下：

空间重采样

空间重采样要复杂一些，主要是因为它考虑到了临近像素的几何差异，因此不能直接从 temporal reservoir buffer 中取出相邻像素的 sample point 然后混合，需要额外注意两点：

• 如果两个像素的几何差异太大则直接丢弃，类似 ReSTIR DI.

• 从像素 \(r\) 去重采样像素 \(q\) 的 sample point 时，因为从两个 visible point 出发生成到同一个 sample point 的采样的概率不同，对应的权重需要除以一个 Jacobian Determinant [这部分来自 Gradient-domain Path Tracing，我没有看懂为什么是这么算的] 来补偿。

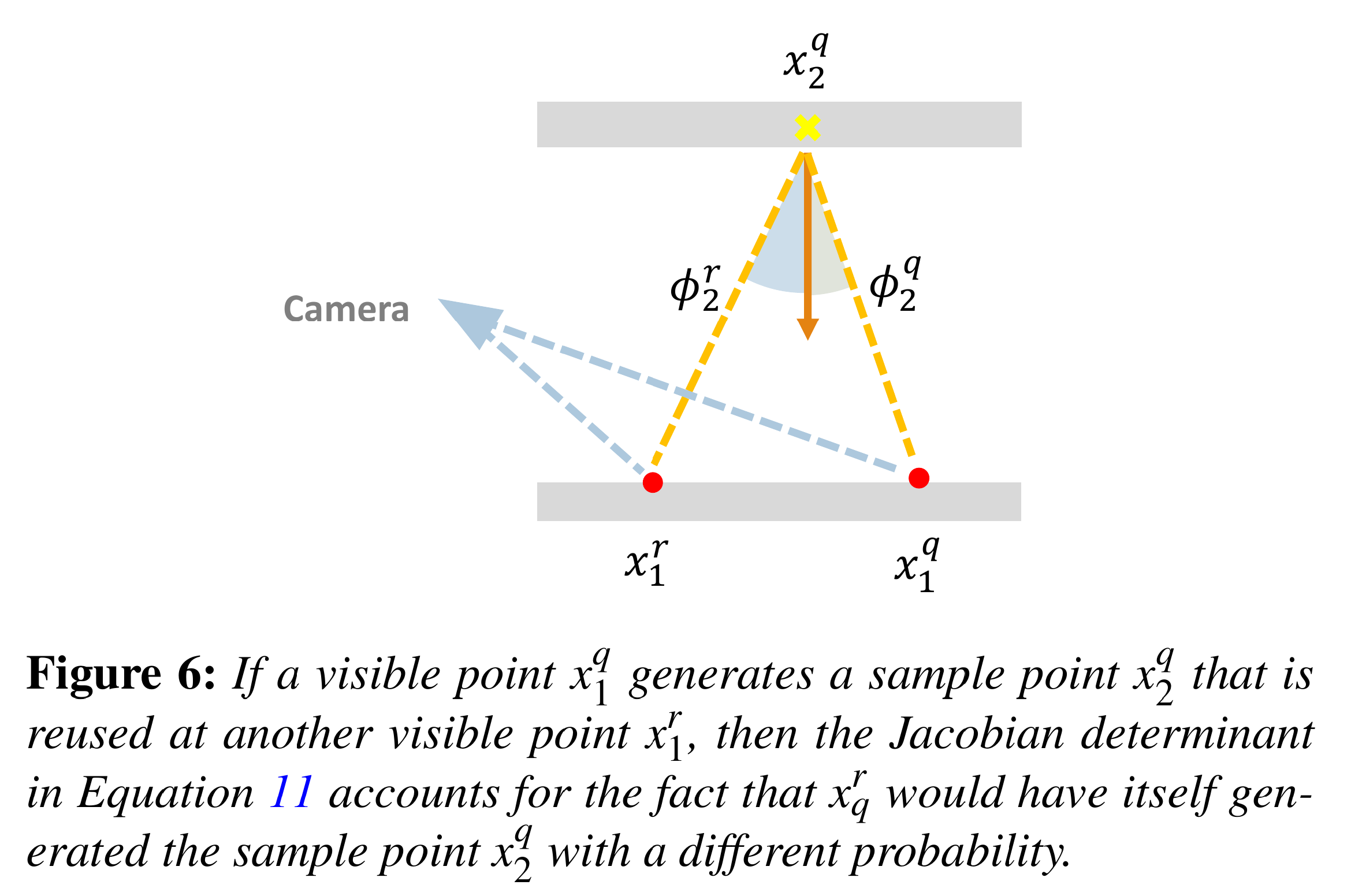
  Jacobian Determinant 的计算公式为 $$ |J_{q\to r}| = \frac{\cos\phi_2^r}{\cos\phi_2^q}\cdot\frac{|x_1^q-x_2^q|}{|x_1^r - x_2^q|} $$ 其中 \(x_1^*\) 表示 visible point，\(x_2^*\) 表示 sample point，示意图见下：

考虑到以上两点之后的伪代码为

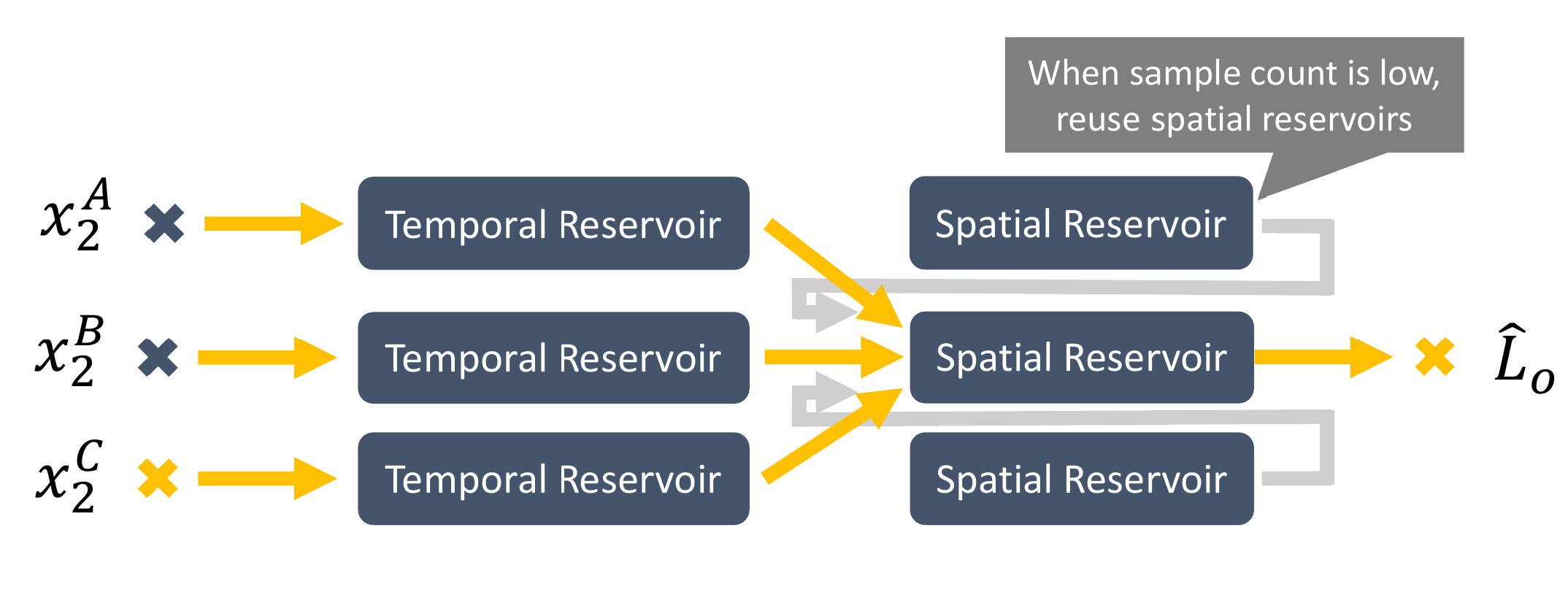
此外，为了避免重复采样导致 bias 累加，ReSTIR GI 在多次空间重采样的时候优先从临近像素的 temporal reservoir buffer 里采样，如果采样数不足才去 spatial reservoir buffer 里采。