Paper Note: Generalized Resampled Importance Sampling - GRIS theory

October 15, 2024 · 茨月

This article is primarily divided into two parts: the first part supplements the sampling theory of ReSTIR, positioning itself as an extension of the RIS theory in Importance Resampling for Global Illumination, and proposes the so-called GRIS or Generalized RIS theory. The second part applies this theory to path reuse and introduces ReSTIR PT.

This note focuses on the discussion of GRIS theory.

Fundamentals of RIS Theory

Background

Rendering is essentially integration. To integrate a function $f$ (i.e., compute $I = \int_\Omega f(x) \text{d}x$), we need to use a Monte Carlo (MC) integrator, where we first sample points and then compute:

$$ \langle I\rangle = \sum_{i=1}^M \frac{f(X_i)}{p(X_i)} $$

As long as the support of the distribution $p$ covers the support of the function $f$, we have:

$$ E[\langle I \rangle] = \int_\Omega f(x)\text {d}x $$

This ensures an unbiased estimate. However, the greater the difference between $p$ and $f$, the higher the variance of the MC integration. This variance manifests as noise in the rendered result. Therefore, we want the distribution $p$ to approximate $f$ as closely as possible.

Problem - Identical Distributions for All Samples

Given a set of samples $X_1, X_2, ..., X_M$, where all samples are independent and identically distributed according to $p$, we want to resample $Y$ from these samples based on certain weights $w_i$, such that the probability density of $Y$ approximates the target function $\hat p = f$.

We define the weights as:

$$ w_i = \frac{1}{M} \hat p(X_i) W_i $$

where:

$$ W_i = \frac{1}{p(X_i)} $$

Sampling $Y$ from $X_1, X_2, ..., X_M$ according to the weights $w_i$, we define the unbiased contribution weight as:

$$ W_Y = \frac{1}{\hat p(Y)} \sum_{i=1}^M w_i $$

As long as the support of the random variable $Y$ covers the support of the function $f$, we have $E[f(Y)W_Y] = I$.

Proof of Correctness

$$ \begin{aligned} E[f(Y)W_Y] &= E\left[f(Y) \cdot \frac{1}{\hat p(Y)} \cdot \sum_{i=1}^M w_i\right] \\ &= E\left[ \sum_{i=1}^M w_i \cdot \frac{f(X_i)}{\hat p(X_i)} \right] \\ &= \frac{1}{M} E\left[ \sum_{i=1}^M\frac{f(X_i)}{p(X_i)} \right] \\ &= \frac{1}{M} \sum_{i=1}^M E\left[ \frac{f(X_i)}{p(X_i)} \right] \\ &= \int_\Omega f(x) dx \end{aligned} $$

Thus, the sampling remains unbiased.

Problem - Generalization, Different Distributions for Each Sample

Given a set of samples $X_1, X_2, ..., X_M$, where $X_i$ is distributed according to $p_i$, we want to resample based on certain weights $w_i$ such that the resampled probability density approximates the target function $\hat p$.

To balance across different distributions, we introduce the MIS (Multiple Importance Sampling) weight:

$$ m_i(x) = \frac{p_i(x)}{\sum_{j=1}^M p_j(x)} $$

It naturally satisfies $\sum_{i=1}^M m_i(x) = 1$. With MIS, the weights are defined as:

$$ w_i = m_i(X_i) \hat p(X_i) W_i $$

where:

$$ W_i = \frac{1}{p_i(X_i)} $$

Degenerate Case:

When all $p_i = p$, $m_i = \frac{1}{M}$, and the MIS case degenerates to the naive case described earlier.

The unbiased contribution weight remains unchanged, and we still have $E[f(Y)W_Y] = I$.

Proof of Correctness

$$ \begin{aligned} E[f(Y)W_Y] &= E\left[f(Y) \cdot \frac{1}{\hat p(Y)} \cdot \sum_{i=1}^M w_i\right] \\ &= E\left[ \sum_{i=1}^M w_i \cdot \frac{f(X_i)}{\hat p(X_i)} \right] \\ &= E\left[ \sum_{i=1}^M m_i(X_i)\frac{f(X_i)}{p_i(X_i)} \right] \\ &= \sum_{i=1}^ME\left[ m_i(X_i)\frac{f(X_i)}{p_i(X_i)} \right]\\ &= \sum_{i=1}^M \int_\Omega m_i(x)\frac{f(x)}{p_i(x)} \cdot p_i(x) \text{d} x \\ &= \sum_{i=1}^M\int_\Omega m_i(x) f(x) \text{d} x \\ &= \int_\Omega \sum_{i=1}^M m_i(x) f(x) \text{d} x \\ &= \int_\Omega f(x) \text{d}x \end{aligned} $$

Notes:

The interchange of summation and expectation is due to the independence of the samples.
The integration domains for different samples are not identical. To ensure correctness, the support must cover the target function:

That is, the union of the supports of all $p_i$ must cover the support of $f$, i.e., $\forall x \in \text{supp}(f), \exists, p_i ; \text{s.t. } x\in \text{supp}(p_i)$.

Generalized RIS

Building on multi-distribution RIS, this paper introduces Generalized RIS to address reuse across different domains.

Background

In simple cases (e.g., ReSTIR DI), the sampling target is the light source distribution, and the target domain for different pixels is identical. However, in more complex reuse scenarios, such as path reuse with ReSTIR, the sampling target is the path space for each pixel, which clearly differs between neighboring pixels. In such cases, we need a way to map samples from other spaces to our target space, known as shift mapping.

Formal Definition

Assume $f$ is defined on $\Omega$. To reuse a sample $X_s \in \Omega_s$, we need to define a shift mapping $T: \Omega_s \to \Omega$.

The mapping must satisfy the following:
- (If an element $x$ has a map) It must be deterministic, one-to-one, and reversible.
- (If an element $x$ does not have a map) No other element can map to $x$.
Essentially, this is a bijection from a subset of $\Omega_s$ to a subset of $\Omega$, but it can have "holes."

With $T$, the weights are further defined as:

$$ w_i = m_i(T_i(X_i)) \hat p(T_i(X_i)) W_i \cdot |\partial T_i/\partial X_i| $$

Note the Jacobian determinant of $T_i$ here!

We sample from the mapped samples $Y_1, Y_2, ..., Y_M$, where $Y_i = T_i(X_i)$, and the weights are $w_i$.

The definition of $W_i$ remains unchanged:

$$ W_i = \frac{1}{p_i(X_i)} $$

The unbiased contribution weight remains unchanged, and we still have $E[f(Y)W_Y] = I$.

Degenerate Case:

If $\Omega_i = \Omega$ and $T = id$, then Generalized RIS degenerates to RIS.

Proof of Correctness

$$ \begin{aligned} E[f(Y)W_Y] &= E\left[f(Y) \cdot \frac{1}{\hat p(Y)} \cdot \sum_{i=1}^M w_i\right] \\ &= E\left[ \sum_{i=1}^M w_i \cdot \frac{f(X_i)}{\hat p(X_i)} \right] \\ &= E\left[ \sum_{i=1}^M m_i(T_i(X_i)) f(T_i(X_i)) \left|\frac{\partial T_i}{\partial x}\right|\right] \\ &= \sum_{i=1}^ME\left[ m_i(T_i(X_i)) f(T_i(X_i)) \left|\frac{\partial T_i}{\partial x}\right|\right] \\ &= \sum_{i=1}^M \int_{\Omega_i} m_i(T_i(x)) f(T_i(x)) \left|\frac{\partial T_i}{\partial x}\right| \text{d} x \\ &= \sum_{i=1}^M \int_{\Omega} m_i(y) f(y) \text{d} y \\ &= \int_{\Omega} \sum_{i=1}^M m_i(y) f(y) \text{d} y \\ &= \int_{\Omega} f(y) \text{d} y \end{aligned} $$

Key points:

The interchange of summation and expectation is due to the independence of the samples.
The substitution step applies the change-of-variables formula, where $y = T_i(x)$, and the Jacobian perfectly accounts for $\text{d} y$.
The final step requires that the union of the images of $T_i$ covers $\Omega$.
- In practical applications, each pixel has its own sample, so there is always at least one $\Omega_i = \Omega, T_i = id$. Thus, this condition is theoretically guaranteed.

Necessity of MIS with Shift Mapping

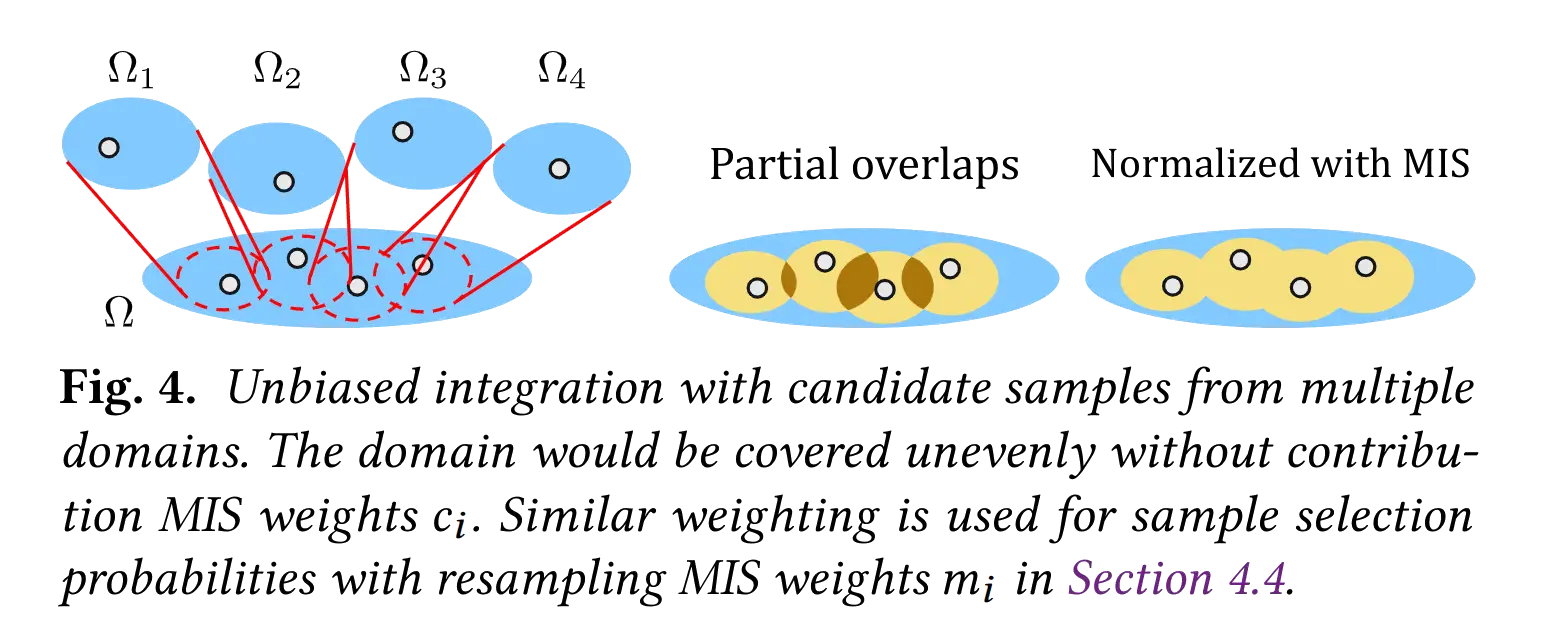
A sample in $\Omega$ may come from multiple $\Omega_i$, so MIS is necessary for balancing. Otherwise, the estimator $\frac{f(Y)}{p_Y(Y)}$ in our MC integrator will have an inaccurate $p_Y$, leading to bias.

ReSTIR - As Chained GRIS

Using the extended GRIS, ReSTIR can be described as a GRIS chain:

Let $Y_i^{t-1}$ be a path for pixel $i$ at frame $t-1$ (either sampled or resampled). The reservoir stores its unbiased contribution weight $W_{Y_i^{t-1}}$. At frame $t$, we proceed as follows:

(Initial Sampling): For each pixel $i$, sample an independent sample $X_i^t$ for the current frame and compute its contribution weight $W_{X_i^t}$.
(Temporal Reuse): Use GRIS to resample between $Y_i^{t-1}$ and $X_i^t$ to obtain $Z_i$ — potentially applying motion vector warping to the old pixel.
(Spatial Reuse): For each pixel, select some neighbors $j$ and perform GRIS resampling between $Z_i$ and the neighbors' $Z_j$ to obtain $Y_i^t$.
(Output): Compute $f_i(Y_i^t) W_{Y_i^t}$ as the estimate of the integral.