Paper Note: ReSTIR GI: Path Resampling for Real-Time Path Tracing

August 6, 2023 · 茨月

This article discusses ReSTIR GI, an algorithm that uses the ReSTIR method to maintain probe sampling for handling 1-bounce global illumination.

Preface

This work extends the ReSTIR sampler, enabling ReSTIR to be applied to global illumination. The article is relatively simple and short, and it doesn’t introduce much theoretical innovation (which might be why it was published in HPG instead of SIGGRAPH).

Update as of Dec. 2024

I don't mean to undermean the contribution of this work. It has been used in the latest AAA games and is both very effective and efficient with diffuse GI. However on a research perspective, I view it more like a "porting this onto that" follow-up-ish work.

In simple terms, the algorithm first generates a G-Buffer containing the spatial positions and local normals of visible points for each pixel (via rasterization or ray tracing for direct lighting). Then, from each visible point, it randomly samples an incident point for indirect light as a sample point, and happily applies ReSTIR to these sample points.

Interestingly, the target distribution for ReSTIR GI sampling can be very simple (e.g., directly set as $\hat p\propto L_o(x_s,-\omega_i)$, without including BRDF or cosine terms) and still achieve good results. The authors explain that a simple target distribution makes the samples generated by one pixel more effective for other pixels. Additionally, since the $L_o$ of the sample point is cached, the authors have to assume that $L_o$ remains unchanged when the sample point connects to different visible points—this assumption is false when the sample point is in non-diffuse media, and artifacts may occur if the scene contains many glossy surfaces.

Algorithm Workflow

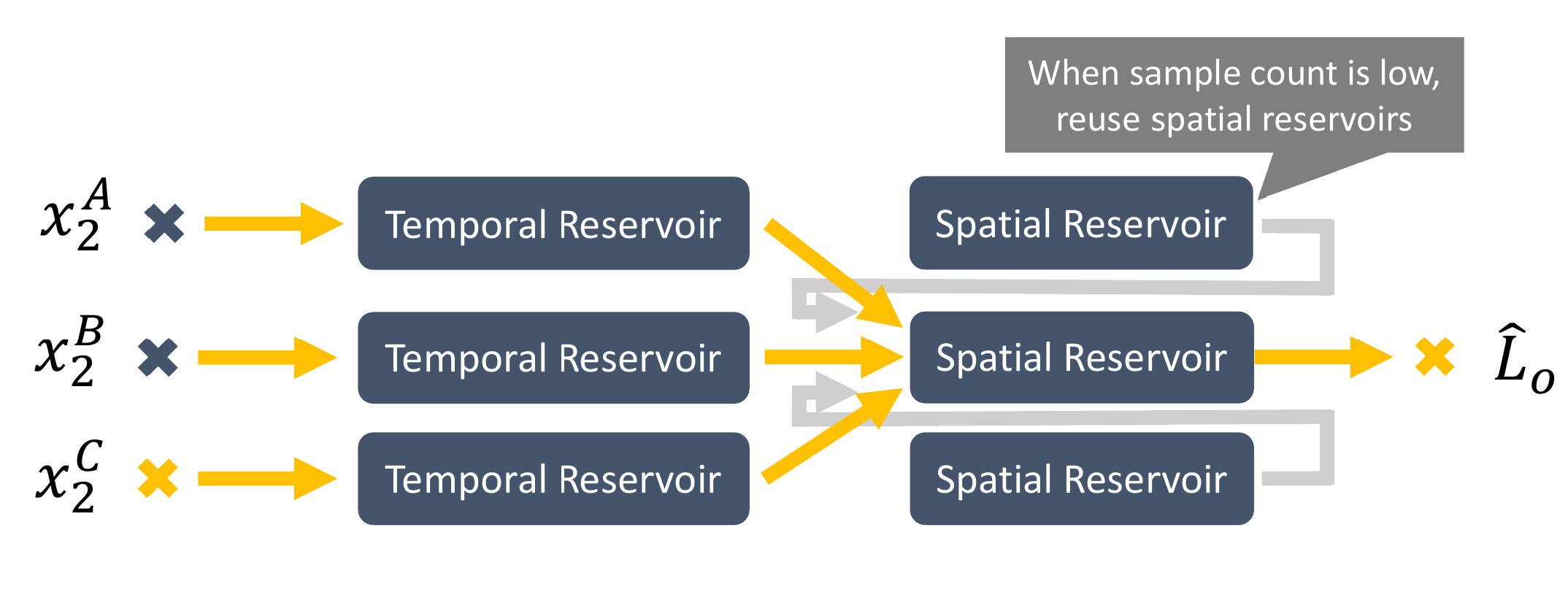
Unlike ReSTIR DI, ReSTIR GI requires maintaining three image-sized buffers: one for storing the initial samples generated in the current round (initial sample buffer), one for the temporal reservoir from the previous round (temporal reservoir buffer), and one for storing neighboring pixel sampling information (spatial reservoir buffer).

The SAMPLE data structure for each pixel is defined as follows, and each buffer consists of width * height SAMPLE instances.

Layout of the SAMPLE data structure for each pixel

To perform ReSTIR GI calculations, the algorithm first needs a G-Buffer that stores the positions and normals of the shading points (called visible points) for each pixel. Each round of the algorithm consists of three steps:

Initial Sampling
Temporal Resampling
Spatial Resampling

The overall workflow of the algorithm can be described by these two diagrams:

Initial Sampling

From each visible point, sample a direction $\omega_i$ using the initial distribution $p_q$. $p_q$ can be a very crude distribution, such as BRDF, cosine-weighted, or even uniform sampling. Trace from the visible point $x_v$ in the direction $\omega_i$ to obtain the intersection point $x_s$, which serves as the sample point for pixel $q$.

Next, the algorithm estimates the outgoing radiance $L_o$ from $x_s$ in the direction $-\omega_i$ (toward $x_v$) as the indirect illumination received by $x_v$. If $L_o$ is computed using direct lighting, the algorithm yields 1-bounce GI; if $L_o$ is computed using $n$-bounce PT with NEE, the algorithm yields $n+1$-bounce GI. Note that $L_o$ is stored as a single value without direction, so when $x_s$ connects to other pixels’ $x_v$, the same value is used—this assumes that $L_o$ is the same in different directions.

The results of the initial sampling are stored in the initial sample buffer.

The pseudocode for initial sampling is as follows:

Temporal Resampling

To perform resampling, the target distribution $\hat p$ must first be determined. It can be the ideal $\hat p\propto L_o(x_s,\omega_i)f(\omega_o,\omega_i)\langle\cos\theta_i\rangle$ (similar to ReSTIR DI) or the simpler $\hat p\propto L_o(x_s,\omega_i)$.

Temporal resampling simply takes the temporal reservoir buffer, mixes it with the corresponding reservoir in the initial sample buffer, and places it back in its original position. The pseudocode is as follows:

Spatial Resampling

Spatial resampling is more complex because it considers geometric differences between neighboring pixels. Therefore, it cannot directly take sample points from adjacent pixels in the temporal reservoir buffer and mix them. Two additional points need to be considered:

If the geometric difference between two pixels is too large, the sample is discarded, similar to ReSTIR DI.
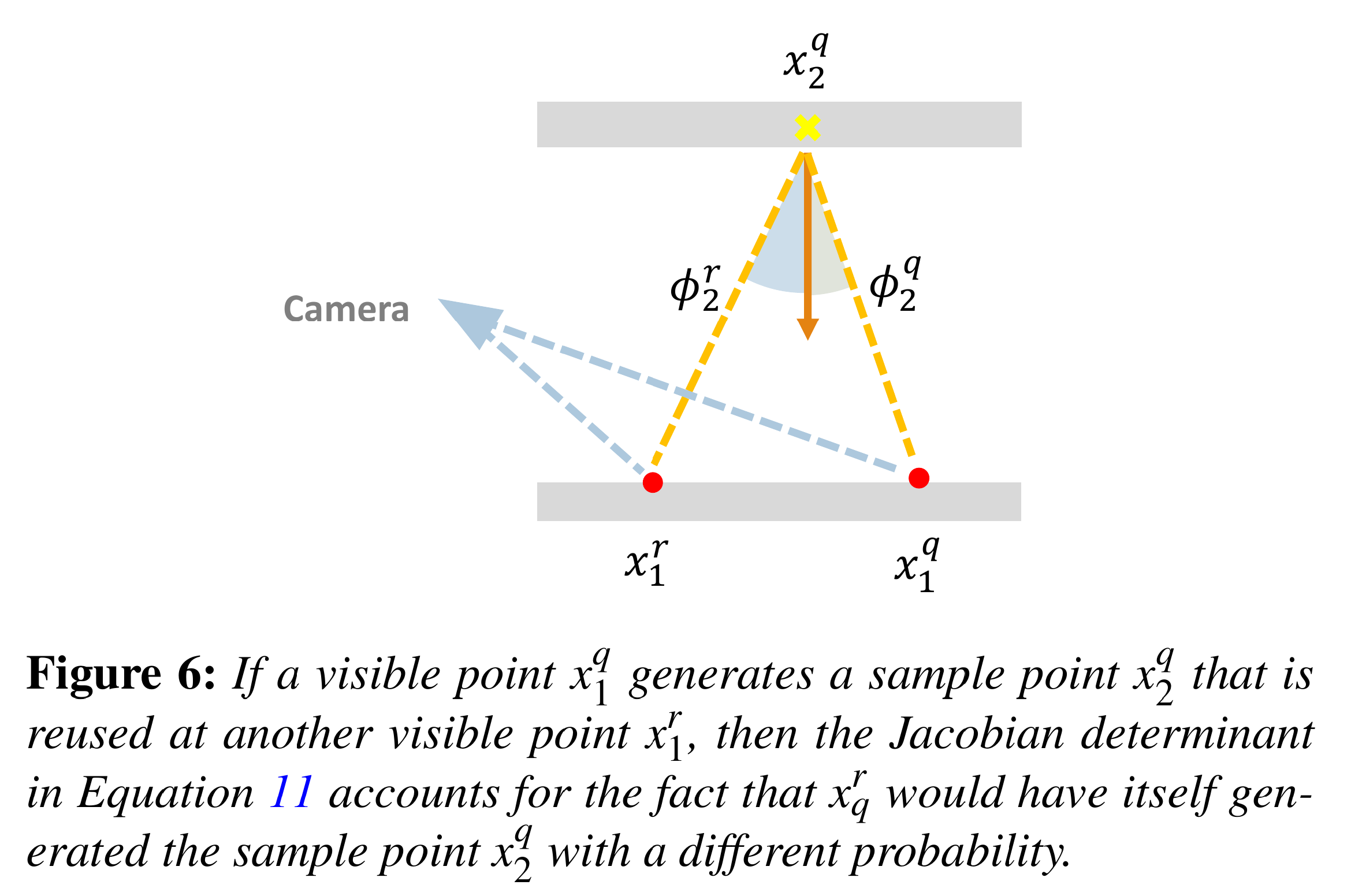
When resampling a sample point from pixel $r$ to pixel $q$, since the probability of generating a sample to the same sample point from two visible points is different, the corresponding weight needs to be divided by a Jacobian Determinant [this part comes from Gradient-domain Path Tracing, and I didn’t understand why it’s calculated this way] to compensate.

The formula for the Jacobian Determinant is: $$ |J_{q\to r}| = \frac{\cos\phi_2^r}{\cos\phi_2^q}\cdot\frac{|x_1^q-x_2^q|}{|x_1^r - x_2^q|} $$ where $x_1^*$ represents the visible point, and $x_2^*$ represents the sample point. The diagram is as follows:

The pseudocode, considering the above two points, is as follows:

Additionally, to avoid bias accumulation from repeated sampling, ReSTIR GI prioritizes sampling from the temporal reservoir buffer of neighboring pixels during multiple spatial resampling steps. If the number of samples is insufficient, it then samples from the spatial reservoir buffer.